Ctrl+K

10. Differential-Algebraische Gleichungen (2)

10. Differential-Algebraische Gleichungen (2)#

In dieser Übung wird das Schwingen eines Pendels simuliert. Dabei ist es möglich, die Bewegung als ODE- oder auch als DAE-System zu beschreiben. Wie unterscheiden sich das jeweils resultierende System und dessen Ergebnisse?

Situation#

Die Bewegung eines Pendels kann sowohl als gewöhnliche Differentialgleichung (ODE) sowie auch als Differential-Algebraisches System (DAE) beschrieben werden.

1. Programmimplementierung#

Lösen Sie die Pendelbewegung mithilfe von ein_pendel_dae.m.

Pendel 
%% file ein_pendel_dae.m
% if your Octave kernel does not plot, write `graphics_toolkit("gnuplot")`
global g m
g = 9.81; l = 0.15; m = 0.05;
y0 = [l 0 0 0 1]; tspan = [0, 3];
M = eye(5); M(5,5) = 0;
options = odeset('Mass',M,'RelTol',1.0e-5,'Stats','on');
tic
[t,y] = rodasp2(@dgl, tspan, y0,options);
toc
axis equal; hold on;
lges=1.2*l; r1 = 0.005; d1=2*r1;
axis ([-lges lges -lges 0.1*lges])
linie1 = line([0 y0(1)],[0 y0(3)]);
kugel1 = rectangle ('Position',[y0(1)-r1 y0(3)-r1 d1 d1],...
'Curvature', [1 1], 'Facecolor', 'r');
for i = 1:length(t)
    set(kugel1, 'Position', [-r1+y(i,1) -r1+y(i,3) d1 d1]);
    set(linie1, 'Xdata', [0 y(i,1)], 'Ydata', [0 y(i,3)]);
    drawnow
    if(i<length(t)) pause ((t(i+1)-t(i)));
    end
end

function dz = dgl(t,z)
    global g m
    dz(1,1) = z(2);
    dz(2,1) = 2*z(5)*z(1)/m;
    dz(3,1) = z(4);
    dz(4,1) = -g + 2*z(5)*z(3)/m;
    % dz(5,1) = z(1)^2 + z(3)^2-l^2; %Index = 3
    % dz(5,1) = z(1)*z(2) + z(3)*z(4); %Index = 2
    dz(5,1) = 2*(z(2)^2+z(1)*dz(2,1)+z(4)^2+z(3)*dz(4,1)); %Index
end

Die Funktion rodasp2 finden Sie hier.

2. Pendellänge#

Leiten Sie aus den Simulationsergebnissen die Pendellänge her und überprüfen Sie, ob sie sich mit der Zeit verändert.

Plotten Sie die eventuelle Längenänderung über die Simulationszeit.

% if your Octave kernel does not plot, write `graphics_toolkit("gnuplot")`
% your code here

3. Systemdämpfung#

Bringen Sie eine Dämpfung in das System ein.

4. Pendel als ODE#

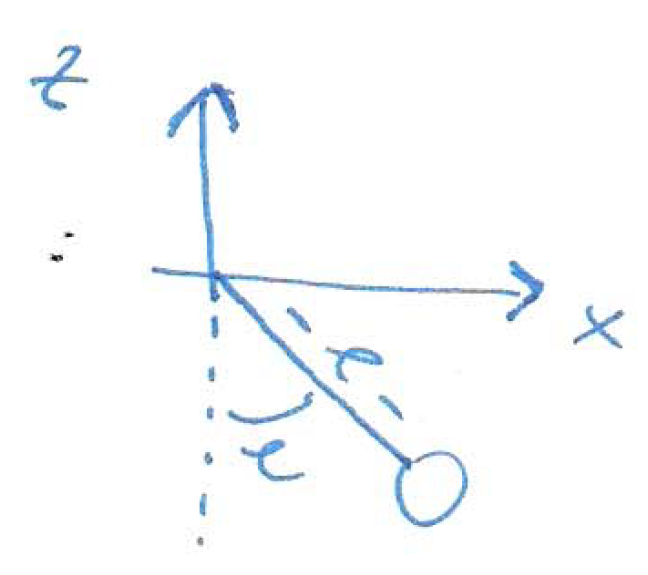
Das Pendel kann auch als ODE beschrieben werden (Drehbewegung). Der Drehwinkel definiert sich dann wie folgt:

\[\ddot{\varphi}=-\frac{g}{L}\sin(\varphi)\]

Dabei ist der Winkel so festgelegt, dass \(\varphi(t)=0\) für ein senkrecht nach unten zeigendes Pendel gilt. Implementieren Sie diese Gleichung und vergleichen Sie die Lösungen der beiden Ansätze.

% your code here

Lösung#

- Hinweis: Dieses Video ist von YouTube aus eingebunden und nicht Teil des frei lizenzierten Materials! -

Zusatzaufgabe: Doppelpendel#

Leiten Sie die Gleichungen eines Doppelpendels her und implementieren Sie diese.

Contents