3. Polynomfitting#
Ziel dieser Übung ist das Fitting von Messdaten mittels Polynomen. Dazu sollen die Benutzer:innen im zu schreibenden Programm die notwendigen Stützstellen per Mauseingabe vorgeben können. Anschließend soll ein Polynom mit frei wählbarem Grad an die Messwerte gefittet werden.
Situation#
Für ein Simulations- und Optimierungsprogramm müssen Messwertverläufe in Form von Kennlinien bereitgestellt werden (Polynome).
Zunächst muss dazu ein Programm geschrieben werden, welches Polynome eines beliebigen Grades auf Basis von gegebenen Stützpunkten berechnet.
Diese Stützpunkte sollen dann vorerst von den Benutzer:innen händisch vorgegeben werden können.
Zum Abschluss sollen optimale Polynome mit vorgefertigten Matlab-Routinen berechnet werden.
1. Polynomgenerator#
Erzeugen Sie ein neues Skript und legen Sie dort eine neue Function main an.
Legen Sie außerdem eine Variable n für den Grad der zu erzeugenden Polynome an.
Erzeugen Sie nun \(n+1\) zufällige x- sowie y-Werte.
%% file main.m
x = 10*rand(n+1,1);
Legen Sie nun eine weitere Function fitpoly mit drei Eingabe- und einem Rückgabewerten an.
Die Funktion soll am Ende dynamisch die Polynomkoeffizienten ermitteln.
%% file fitpoly.m
% x – x-Werte, y – y-Werte, n – Grad des Polynoms
function p = fitpoly(x,y,n)
% your code here
Polynome haben generell folgende Form (\(n+1\) Koeffizienten bei Grad \(n\)):
Bei Eingabe eines der x-Werte soll das Polynom den entsprechenden y-Wert zurückgeben. Dadurch ergibt sich ein lineares Gleichungssystem (LGS).
Stellen Sie dieses LGS in Matrix-Form (\(Ax = b\)) auf und versuchen Sie dessen Struktur in das Matlab-Skript zu übertragen. Wie kann die Matrix \(A\) abhängig von \(n\) dynamisch erstellt werden?
In der Variablen \(p\) sollen schließlich die ermittelten Koeffizienten zurückgegeben werden.
Tipp
Nutzen Sie eine for-Schleife zur Erzeugung der Matrix.
2. Polynomevaluierung#
Um die Richtigkeit der berechneten Koeffizienten zu prüfen wird eine Funktion benötigt, welche die ermittelten Polynome an den entsprechenden x-Werten auswertet.
Legen Sie dazu eine neue Function evalpoly mit zwei Eingangs- und einem Rückgabewert an.
%% file evalpoly.m
% p – Polynomkoeffizienten, x - Abfragestellen
function y = evalpoly(p,x)
% your code here
Für die Polynome gilt allgemein weiterhin die o.g. Formel. Erzeugen Sie also ein Programm, welches basierend auf einer variablen Anzahl von Polynomkoeffizienten entsprechende y-Werte berechnet und zurückgibt.
Benutzerdefinierte Polynome#
Laden Sie die Messwerte in Ihr Programm (in der main-Function) und plotten Sie diese.
Anschließend soll mittels der Funktion ginput eine Benutzereingabe möglich sein, über welche die Polynomstützpunkte händisch definiert werden.
Diese sollen schließlich ausgewertet und das entsprechende Polynom geplottet werden.
Pseudocode:
% Hauptprogramm
function main
n = 3; % Gewünschter Grad des Polynoms
Import der Messwerte
% Öffnen eines figure-Fensters und ggf. Löschen von
% bestehendem Inhalt
figure(1)
clf
Plotten der Messwerte
hold on
i = 1; % Zählvariable
while i<n
1: Abfragen Mausklick mit „ginput“ und Speichern von x- und y-Koordinaten in Matrix
2: Plot des Klicks mit rotem „X“
i = i+1;
end
1: Aufruf von „fitpoly“ mit den eingegebenen x/y-Koordinaten und Rückgabe der Polynomkoeffizienten p
2: Aufruf von „evalpoly“ zur Auswertung des Polynoms p an allen gemessenen x-Werten
3: Plot des Polynoms
end
% Berechnet Polynomkoeffizienten vom Grad n
function p = fitpoly(x,y,n)
Berechnung der Polynomkoeffizienten nach Aufgabe 1
end
% Wertet Polynom mit Koeffizienten p an Stellen x aus
function y = evalpoly(p,x)
Ermittlung der Funktionswerte von p an Stelle x
end
4. Polynomberechnung mit der Matlab-Routine polyfit#
Ähnlich der eingangs erstellten Funktionen arbeiten auch die Matlab-Routinen polyfit und polyval. Der Vorteil liegt u.a. darin, dass polyfit für ein Polynom vom Grad \(n\) auch mehr als \(n+1\) Wertepaare verwenden kann. Polyfit versucht dann den Abstand zwischen Mess- und Funktionswerten auf ein Minimum zu optimieren.
Lassen Sie nun also für die vorhandenen Messwerte Polynome mittels polyfit berechnen, werten diese mit polyval zu den gemessenen Zeitpunkten aus und plotten das Resultat über die ursprünglichen Werte.
% Erzeugt Polynom vom Grad n basierend auf x/y-
% Wertepaaren
p = polyfit(x,y,n);
% Wertet Polynom p an den entsprechenden x-Stellen aus
y = polyval(p,x);
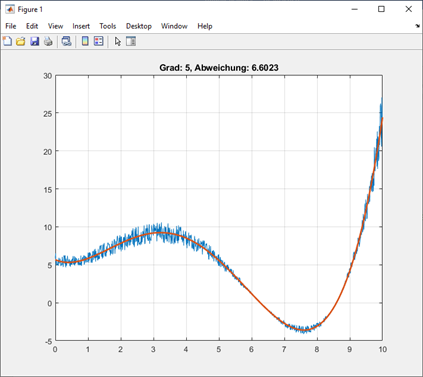
5. Zusatz: Güte-Berechnung#
Berechnen Sie die Güte der erzeugten Polynome (sowohl benutzerdefiniert als auch mit polyfit). Ein Maß dazu ist der Abstand zwischen Mess- und berechneten Werten.
Nutzen Sie dazu die Formel des quadratischen Mittels:
% your code here

