Stabilität des expliziten versus impliziten Eulerverfahrens

Stabilität des expliziten versus impliziten Eulerverfahrens#

Bestimmte ODEs lassen sich mit impliziten Verfahren besser lösen als mit expliziten Verfahren. Diese ODEs bezeichnen wir als steif. Das möchten wir an einem kleinen Modellproblem demonstrieren.

Entscheidend dafür ist, ob eine hohe maximale Steigung vorliegt. Diese wird mit der Lipschitzkonstanten beschrieben, die eine obere Schranke der Steigung \(f_y\) aufstellt (mit der ODE \(y' = f(t,y)\)).

\[\forall y_1,y_2 \in \mathbb{D} : \left(L \ge \left|\frac{f(t,y_1)-f(t,y_2)}{y_1-y_2}\right|\right)\]

. Je höher die Lipschitz-Konstante, desto kleiner muss oft die notwendige Schrittweite \(h\) gewählt werden. Für das explizite Eulerverfahren gilt \(h<\frac{2}{|L|}\).

Stabilität der Dahlquist- und Prothero-Robinson-Gleichungen#

Ein geeignetes Stabilitätsproblem ist die inhomogene Prothero-Robinson-Gleichung mit

\[y'=-λ(y-g)+g',\quad y(0)=y_0,\quad g(0)=g_0,\quad λ>0.\]

\(g(t)\) ist eine glatte Funktion.

Die analytische Lösung lautet \(y(t) = e^{-\lambda t}(y_0-g_0) + g(t)\). Für \(λ≫1\) konvergiert \(y(t)\) schnell gegen \(g(t)\). Außerdem ist die Lipschitzkonstante leicht zu ermitteln mit \(|y'|_\text{max} = \lambda\), also \( h < \frac{2}{\lambda} \) für das explizite Eulerverfahren.

Für \(g(t) = 0\) entspricht die Prothero-Robinson-Gleichung der Dahlquist-Gleichung, also der ODE der Form \(y'=-λy,λ>0,y_0=1\) mit der exakten Lösung \(y(t)=e^{-λt}\).

Für \(g(t) = const.\) lautet die DGL \(y' = -\lambda (y - g)\) mit der Lösung \(y(t) = g + e^{-λt}\), die gegen \(g\) konvergiert. Bei Anwendung des impliziten Eulerverfahrens erhalten wir \(y_{k+1} = \frac{y_k + h\lambda g}{1+h\lambda}\).

Herleitung von \(y_{k+1}\)

Für das implizite Eulerverfahren lautet die Forschrift allgemein

\[y_{k+1} = y_k + h\cdot y'_{k+1}.\]

In diesem Fall erhalten wir

\[y_{k+1} = y_k + h\cdot(-\lambda(y_{k+1}-g)) \to y_{k+1}(1+h\lambda) = y_k + h\lambda g \to y_{k+1} = \frac{y_k + h\lambda g}{1+h\lambda}\]

Aufgabe 1#

Weisen Sie nach, dass \(y(t)=g(t)+e^{-λt} (y_0-g_0)\) die exakte Lösung der ODE für allgemeine \(g(t)\) ist.

Aufgabe 2#

In dieser Übung sollen Sie optisch kennen lernen, wie sich die Lösungen des expliziten und impliziten Eulerverfahrens unterscheiden. Damit können Sie auch ein Gefühl dafür entwickeln, was steife Funktionen auszeichnet.

Mit dem unten stehenden Code können Sie in Octave bzw. Matlab eine App ausführen, die Ihnen erlaubt, die Prothero-Robinson-Gleichung mit dem für Sie fertig implementierten expliziten und impliziten Eulerverfahren zu lösen und die Lösungen zu vergleichen. Sie können die wesentlichen Parameter (\(\lambda, y_0, h_\text{explizit}, h_\text{implizit}\)) mit Schiebereglern variieren.

Variieren Sie nun mithilfe der App die verfügbaren Parameter und die Funktion für \(g(t)\). Gegebenenfalls müssen Sie den Code lokal ausführen.

Wie unterscheiden sich die Lösungen beider Verfahren?
Erkennen Sie für \(t=0\), dass die explizite Lösung immer genau die Steigung der Lösung annimmt?
Was passiert, wenn \(h\) für das explizite Verfahren nur minimal kleiner als \(\frac{2}{|\lambda|}\) ist? Was passiert, wenn \(h\) größer ist?
Bei welchen Parametern ist das explizite Verfahren nicht mehr hilfreich? Was macht die “Steifheit” der resultierenden Funktionen qualitativ aus?

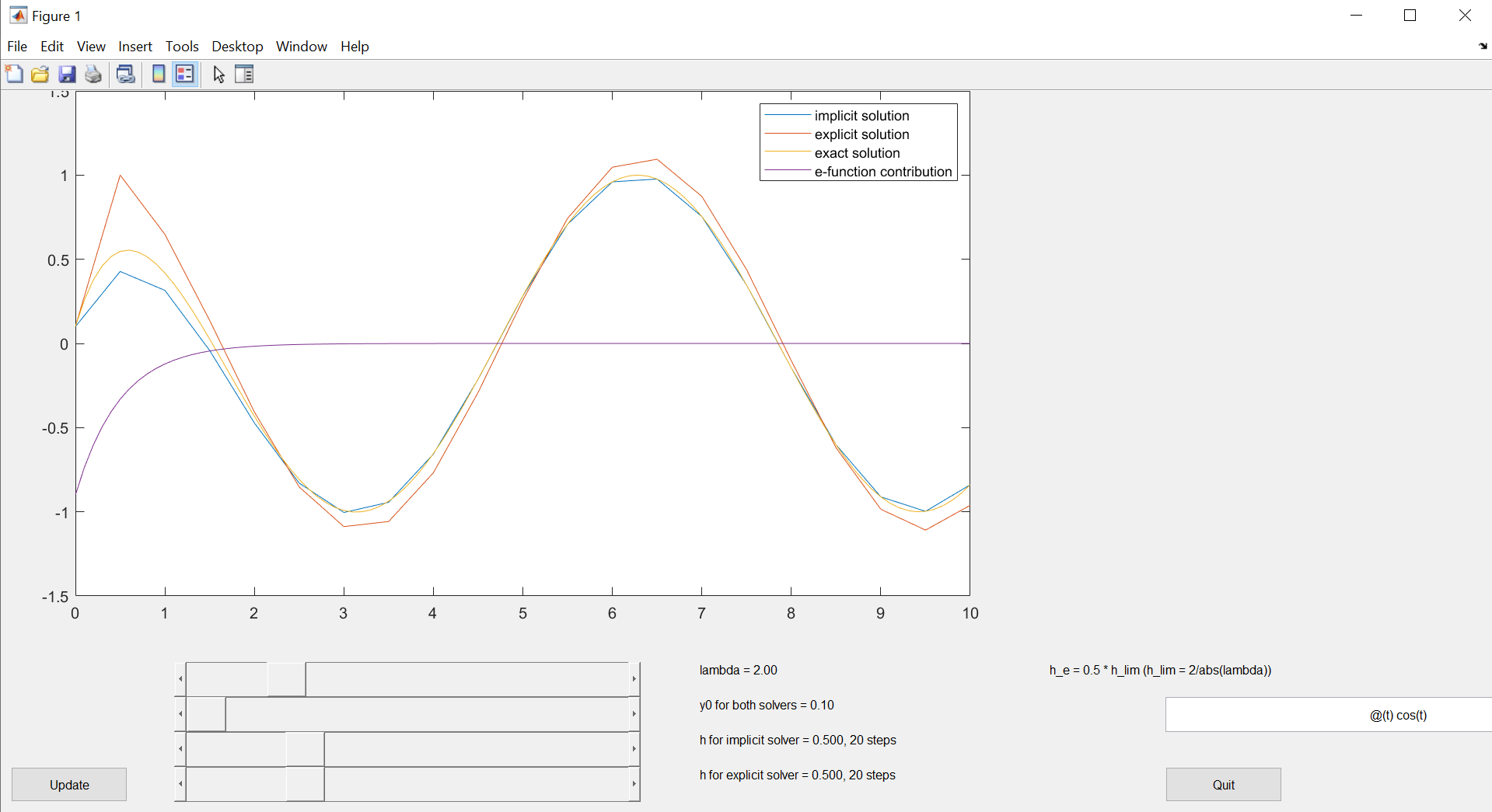
Probieren Sie für \(g(t)\) beispielsweise aus

\(g(t) = 0\) (entspricht der Dahlquist-Gleichung)
\(g(t) = \) t.^2 (da die Rechnung mit Matrizen durchgeführt wird, ist die Punkt-Notation nötig)
\(g(t) = \cos t\)
\(g(t) = \sin t\)
… und was Sie noch interessiert.

Octave Code

Hinweis

Falls Sie Octave von Ihrer Konsole aufrufen, rufen Sie octave --persist <filename> auf, um das Ausgabefenster geöffnet zu halten.

Show code cell source Hide code cell source

%graphics_toolkit (gt)

close all
clearvars

fi.fig = figure(1,'position',[0.5 0.5 1450 700]);
fi.ax = axes("position",[0.05 0.3 0.6 0.7]);

function updatefig(obj, init)
  if nargin <2
    init = false;
  else
    init = true;
  endif
  
  fi = guidata(obj);
  replot = false;
  recalc = false;
  switch (obj)
    case {fi.update_button}
      recalc = true;
      replot = true;
    case {fi.quit_button}  
      close all;  
    case {fi.h_e_slide,fi.h_i_slide,fi.y0_slide,fi.update_button,fi.lambda_slide}
      recalc = true;
    case {fi.g_field}
      recalc = true;
  endswitch
  
  if (recalc || init)
    %% input parameters
    h_e = get(fi.h_e_slide, 'value');
    fi.h_i = get(fi.h_i_slide, 'value');
    y0 = get(fi.y0_slide, 'value');
    fi.lambda = get(fi.lambda_slide, 'value');
    fi.fcn_g = str2func(get(fi.g_field,'string'));
    
    %% explicit form of ODE, g' with finite differences
    fi.fcn_proth = @(t,y) - fi.lambda* (y - fi.fcn_g(t)) + (fi.fcn_g(t+fi.h_i)-fi.fcn_g(t-fi.h_i))/(2*fi.h_i);
    
    %% time scale
    tmin = 0;
    tmax = 10;
    tspan = tmin:0.01:tmax;
    
    %% base function g
    g0 = fi.fcn_g(0);
    
    %% solving with explizit Euler method
    t_e = tmin:h_e:tmax;
    fi.y_e = zeros(size(t_e));
    y_e(1) = y0;
    for i = 2:length(t_e)
        y_e(i) = y_e(i-1) + h_e * fi.fcn_proth(t_e(i-1),y_e(i-1));
    end

    %% solving with implicit Euler method
    t_i = tmin:fi.h_i:tmax;
    y_i=zeros(size(t_i));
    y_i(1)=y0;
    for i = 2:length(t_i)
        y_i(i) = ( y_i(i-1) + fi.h_i*fi.lambda*fi.fcn_g(t_i(i)) + fi.fcn_g(t_i(i))-fi.fcn_g(t_i(i-1))) / (1+fi.h_i*fi.lambda);
    end

    replot = true;
  endif
  
  if (replot)
    fi.plot = plot(t_i,y_i,t_e,y_e,tspan, fi.fcn_g(tspan) + exp(-fi.lambda*tspan)*(y0-g0), tspan, exp(-fi.lambda*tspan)*(y0-g0));
    
    fi.plotlabel = legend('implicit solution', 'explicit solution', 'exact solution', 'e-function contribution');
    
    fi.h_e_label = uicontrol ("style", "text",...
                          "string", sprintf("h for explicit solver = %.3f, %d steps", h_e, tmax/h_e),...
                          "horizontalalignment", "left",...
                          "position", [600,10,400,30]);
    
    fi.h_i_label = uicontrol ("style", "text",...
                          "string", sprintf("h for implicit solver = %.3f, %d steps", fi.h_i, tmax/fi.h_i),...
                          "horizontalalignment", "left",...
                          "position", [600,40,400,30]);
                          
    fi.y0_label = uicontrol ("style", "text",...
                          "string", sprintf("y0 for both solvers = %.2f", y0),...
                          "horizontalalignment", "left",...
                          "position", [600,70,300,30]);
                          
    fi.lambda_label = uicontrol ("style", "text",...
                          "string", sprintf("lambda = %.2f", fi.lambda),...
                          "horizontalalignment", "left",...
                          "position", [600,100,300,30]);
                          
    fi.lambda_check_label = uicontrol ('style', 'text',...
                          'string', sprintf('h_e = %.1f * h_lim (h_lim = 2/abs(lambda))', h_e / (2/abs(fi.lambda))),...
                          'horizontalalignment','left',...
                          'position', [900, 100, 500, 30]);
                          
    fi.g = substr(get(fi.g_field,'string'),6);
    fi.ydot = uicontrol ("style", "text",...
                          "string", sprintf("ODE: y' = -%.1f (y - %s) + [%s]'", fi.lambda, fi.g, fi.g),...
                          "horizontalalignment", "left",...
                          "position", [1000,40,400,30]);
    
    if h_e / (2/abs(fi.lambda)) >= 1
      set (fi.lambda_check_label, 'foregroundcolor', 'red');
      set (fi.lambda_check_label, 'string', sprintf('h_e = %.1f * h_lim (h_lim = 2/abs(lambda)), divergence!', h_e / (2/abs(fi.lambda))));
    endif

  endif
endfunction

fi.update_button = uicontrol('style','pushbutton',...
                      'string','Update',...
                      'callback',@updatefig,...
                      'position',[10,10,100,30]);

fi.quit_button = uicontrol('style','pushbutton',...
                      'string','Quit',...
                      'callback',@updatefig,...
                      'position',[1000,10,100,30]);

fi.h_e_slide = uicontrol('style','slider',...
                      'min',0.01,...
                      'max',2,...
                      'value',0.5,...
                      'callback',@updatefig,...
                      'position',[150,10,400,30]);

fi.h_i_slide = uicontrol('style','slider',...
                      'min',0.01,...
                      'max',2,...
                      'value',0.5,...
                      'callback',@updatefig,...
                      'position',[150,40,400,30]);

fi.y0_slide = uicontrol('style','slider',...
                      'min',0.1,...
                      'max',10,...
                      'value',0.1,...
                      'callback',@updatefig,...
                      'position',[150,70,400,30]);

fi.lambda_slide = uicontrol('style','slider',...
                      'min',0.01,...
                      'max',10,...
                      'value',2,...
                      'callback',@updatefig,...
                      'position',[150,100,400,30]);
                      
fi.g_label = uicontrol ("style", "text",...
                      "string", sprintf("g(t) = "),...
                      "horizontalalignment", "left",...
                      "position", [1000,70,400,30]);

fi.g_field = uicontrol('style','edit',...
                      'string','@(t) cos(t)',...
                      'callback',@updatefig,...
                      'position',[1050,70,350,30]);
                      
set (gcf, "color", get(0, "defaultuicontrolbackgroundcolor"))
guidata(gcf,fi);
updatefig(gcf,true);

Matlab Code

Show code cell source Hide code cell source

% Matlab equivalent

close all
clearvars

fi.fig = figure('position',[0.5 0.5 1450 700]);
fi.ax = axes("position",[0.05 0.3 0.6 0.7]);

fi.update_button = uicontrol('style','pushbutton',...
                      'string','Update',...
                      'callback',@updatefig,...
                      'position',[10,10,100,30]);

fi.quit_button = uicontrol('style','pushbutton',...
                      'string','Quit',...
                      'callback',@updatefig,...
                      'position',[1000,10,100,30]);

fi.h_e_slide = uicontrol('style','slider',...
                      'min',0.01,...
                      'max',2,...
                      'value',0.5,...
                      'callback',@updatefig,...
                      'position',[150,10,400,30]);

fi.h_i_slide = uicontrol('style','slider',...
                      'min',0.01,...
                      'max',2,...
                      'value',0.5,...
                      'callback',@updatefig,...
                      'position',[150,40,400,30]);

fi.y0_slide = uicontrol('style','slider',...
                      'min',0.1,...
                      'max',10,...
                      'value',0.1,...
                      'callback',@updatefig,...
                      'position',[150,70,400,30]);

fi.lambda_slide = uicontrol('style','slider',...
                      'min',0.01,...
                      'max',10,...
                      'value',2,...
                      'callback',@updatefig,...
                      'position',[150,100,400,30]);
                      
fi.g_label = uicontrol ("style", "text",...
                      "string", sprintf("g(t) = "),...
                      "horizontalalignment", "left",...
                      "position", [1000,70,400,30]);

fi.g_field = uicontrol('style','edit',...
                      'string','@(t) cos(t)',...
                      'callback',@updatefig,...
                      'position',[1050,70,350,30]);
                      
set (gcf, "color", get(0, "defaultuicontrolbackgroundcolor"))
guidata(gcf,fi);
updatefig(gcf,true);

function updatefig(obj, init)
  if nargin <2
      init = false;
  else
      init = true;
  end
  
  fi = guidata(obj);
  replot = false;
  recalc = false;
  switch (obj)
    case {fi.update_button}
      recalc = true;
      replot = true;
    case {fi.quit_button}  
      close all;  
    case {fi.h_e_slide,fi.h_i_slide,fi.y0_slide,fi.update_button,fi.lambda_slide}
      recalc = true;
    case {fi.g_field}
      recalc = true;
  end
  
  if (recalc || init)
    %% input parameters
    h_e = get(fi.h_e_slide, 'value');
    fi.h_i = get(fi.h_i_slide, 'value');
    y0 = get(fi.y0_slide, 'value');
    fi.lambda = get(fi.lambda_slide, 'value');
    fi.fcn_g = str2func(get(fi.g_field,'string'));
    
    %% explicit form of ODE, g' with finite differences
    fi.fcn_proth = @(t,y) - fi.lambda* (y - fi.fcn_g(t)) + (fi.fcn_g(t+fi.h_i)-fi.fcn_g(t-fi.h_i))/(2*fi.h_i);
    
    %% time scale
    tmin = 0;
    tmax = 10;
    tspan = tmin:0.01:tmax;
    
    %% base function g
    g0 = fi.fcn_g(0);
    
    %% solving with explizit Euler method
    t_e = tmin:h_e:tmax;
    fi.y_e = zeros(size(t_e));
    y_e(1) = y0;
    for i = 2:length(t_e)
        y_e(i) = y_e(i-1) + h_e * fi.fcn_proth(t_e(i-1),y_e(i-1));
    end

    %% solving with implicit Euler method
    t_i = tmin:fi.h_i:tmax;
    y_i=zeros(size(t_i));
    y_i(1)=y0;
    for i = 2:length(t_i)
        y_i(i) = ( y_i(i-1) + fi.h_i*fi.lambda*fi.fcn_g(t_i(i)) + fi.fcn_g(t_i(i))-fi.fcn_g(t_i(i-1))) / (1+fi.h_i*fi.lambda);
    end

    replot = true;
  end
  
  if (replot)
    fi.plot = plot(t_i,y_i,t_e,y_e,tspan, fi.fcn_g(tspan) + exp(-fi.lambda*tspan)*(y0-g0), tspan, exp(-fi.lambda*tspan)*(y0-g0));
    
    fi.plotlabel = legend('implicit solution', 'explicit solution', 'exact solution', 'e-function contribution');
    
    fi.h_e_label = uicontrol ("style", "text",...
                          "string", sprintf("h for explicit solver = %.3f, %d steps", h_e, tmax/h_e),...
                          "horizontalalignment", "left",...
                          "position", [600,10,400,30]);
                          
    fi.h_i_label = uicontrol ("style", "text",...
                          "string", sprintf("h for implicit solver = %.3f, %d steps", fi.h_i, tmax/fi.h_i),...
                          "horizontalalignment", "left",...
                          "position", [600,40,400,30]);
                          
    fi.y0_label = uicontrol ("style", "text",...
                          "string", sprintf("y0 for both solvers = %.2f", y0),...
                          "horizontalalignment", "left",...
                          "position", [600,70,300,30]);
                          
    fi.lambda_label = uicontrol ("style", "text",...
                          "string", sprintf("lambda = %.2f", fi.lambda),...
                          "horizontalalignment", "left",...
                          "position", [600,100,300,30]);
                          
    fi.lambda_check_label = uicontrol ('style', 'text',...
                          'string', sprintf('h_e = %.1f * h_lim (h_lim = 2/abs(lambda))', h_e / (2/abs(fi.lambda))),...
                          'horizontalalignment','left',...
                          'position', [900, 100, 500, 30]);
                          
    fi.g = extractAfter(get(fi.g_field,'string'),5);
    fi.ydot = uicontrol ("style", "text",...
                          "string", sprintf("ODE: y' = -%.1f (y - %s) + [%s]'", fi.lambda, fi.g, fi.g),...
                          "horizontalalignment", "left",...
                          "position", [1000,40,400,30]);
    
    if h_e / (2/abs(fi.lambda)) >= 1
      set (fi.lambda_check_label, 'foregroundcolor', 'red');
      set (fi.lambda_check_label, 'string', sprintf('h_e = %.1f * h_lim (h_lim = 2/abs(lambda)), divergence!', h_e / (2/abs(fi.lambda))));
    end

  end
end

Hinweis

Die Matlab Dokumentation und zugehörige Blogs liefern weitere anschauliche Beispiele: