Voraussetzungen

• mathematische Grundlagen der Fouriertransformation

Lerninhalte

• Anwendung der Fouriertransformation als Frequenzfilter (digitaler Filter)

Filtern verrauschter Signale

Analysieren Sie das Frequenz- und Amplitudenspektrum des Signals

\[ S = a_1 \sin(2 \pi f_1 t) + a_2 \sin(2 \pi f_2 t) + a_3 \sin(2 \pi f_3 t) \]

mit \(a_1 = 0.3\), \(a_2 = 0.1\), \(a_3=0.4\) und \(f_1 = 50\) Hz, \(f_2 = 40\) Hz und \(f_3 = 30\) Hz und zufällig aufgeprägtem Rauschen. Machen Sie sich dazu mit der Matlab-Funktion fft vertraut und lassen Sie sich das Frequenzspektrum grafisch ausgeben.

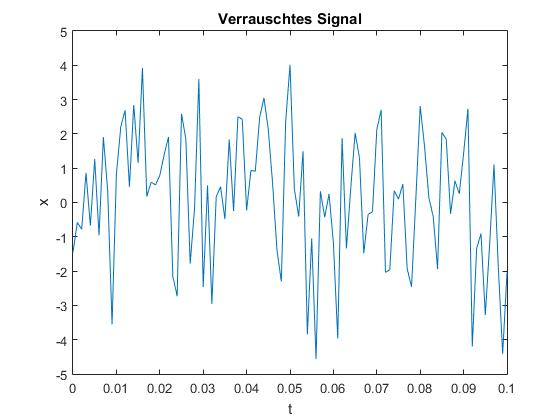
Verwenden Sie dann einen digitalen Filter, um das Rauschen des Signals zu unterdrücken und vergleichen anschließend das gefilterte mit dem unverrauschten Signal S. Wie könnten Sie den Filter konstruieren? Experimentieren Sie mit unterschiedlich stark verrauschten Signalen.

Hinweis

Das Signal mit normalverteiltem Rauschen können Sie wie folgt erzeugen:

t = linspace(0, 0.1, 1000);
S = a1*sin(2*pi*f1*t) + a2*sin(2*pi*f2*t) + a3*sin(2*pi*f3*t);
S_noise = S + sqrt(noise_variance)*randn(size(t));