Voraussetzungen

• Matrizen-Grundlagen

• dynamische Kräfte-Gleichgewichte

Lerninhalte

• Lösung bekannter Modellgleichungen mithilfe von räumlicher Diskretisierung als Modellannahme

• Vergleich und Bewertung iterativer Gleichungssystemlöser

Modellierung einer Highline

- Hinweis: Dieses Video ist von YouTube aus eingebunden und nicht Teil des frei lizenzierten Materials! -

Mittels einer Reihenschaltung von Federdämpfer-Systemen lässt sich ein einfaches zweidimensionales Modell einer Highline erstellen.

Modellbeschreibung

Abbildung 1: Die Highline wird als eine Kette von N Massepunkten modelliert, die jeweils mit Feder- und Dämpferelementen in horizontaler und vertikaler Richtung miteinader verbunden sind.

Kräftebilanzierung

Gehen Sie von einem “Urzustand” aus, in dem alle Massepunkte auf einer Linie liegen. Durch die Schwerkraft und das Einwirken äußerer Kräfte entstehen Verschiebungen \(\mathbf{z}_i = \begin{bmatrix} x_i(t) \\ y_i(t) \end{bmatrix}\) der Massepunkte weg von diesem Urzustand. Die Verschiebungen der Ankerpunkte seien konstant Null, \(\mathbf{z}_{0}=\mathbf{z}_{N+1}=\begin{bmatrix} 0 \\ 0 \end{bmatrix}\).

Angenommen jeder Massepunkt hat die Masse \(m\) und die Federdämpferelemente haben die Steifigkeiten \(k\) und Dämpfungskoeffizienten \(d\). Durch Freischneiden und Kraftbilanzierung lassen sich für alle Massepunkte die Bewegungsgleichungen aufstellen. Sei \(\mathbf{F}_{i,\text{ext}} \in \mathbb{R}^2\) die externe Kraft, die auf den Massepunkt mit Index \(i\) wirkt. Dann gilt

\[\begin{split} \begin{align} m \ddot{\mathbf{z}}_0 &= 0 \notag \\ m \ddot{\mathbf{z}}_1 &= -k \mathbf{z}_1 - d \dot{\mathbf{z}}_1 -k(\mathbf{z}_1-\mathbf{z}_2) - d(\dot{\mathbf{z}}_1-\dot{\mathbf{z}}_2) + \mathbf{F}_{1,\text{ext}} \notag \\ m \ddot{\mathbf{z}}_i &= k(\mathbf{z}_{i-1}-\mathbf{z}_{i}) + d(\dot{\mathbf{z}}_{i-1} - \dot{\mathbf{z}}_{i}) - k(\mathbf{z}_{i}-\mathbf{z}_{i+1}) - d(\dot{\mathbf{z}}_{i} -\dot{\mathbf{z}}_{i+1}) + \mathbf{F}_{i,\text{ext}}, \hskip4em \text{für } i=2,...,N-1 \notag \\ m \ddot{\mathbf{z}}_N &= -k \mathbf{z}_N - d \dot{\mathbf{z}}_N + k(\mathbf{z}_{N-1}-\mathbf{z}_N) + d(\dot{\mathbf{z}}_{N-1}-\dot{\mathbf{z}}_N) + \mathbf{F}_{N,\text{ext}} \notag \\ m \ddot{\mathbf{z}}_{N+1} &= 0 \notag \end{align} \end{split}\]

Diese Gleichungen lassen sich in eine kompaktere Matrixschreibweise bringen. Dazu führen wir folgende Bezeichungen ein:

\[\begin{split} \mathbf{z}=\left[ \begin{array}{c} \mathbf{z}_1 \\ \vdots \\ \mathbf{z}_N \end{array} \right] \in \mathbb{R}^{2N}, \quad \mathbf{F}_{\text{ext}} = \left[ \begin{array}{c} \mathbf{F}_{1,\text{ext}} \\ \vdots \\ \mathbf{F}_{N,\text{ext}} \end{array} \right] \in \mathbb{R}^{2N}, \quad M = \left[ \begin{array}{cccc} m & 0 & \cdots & 0 \\ 0 & m & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & m \end{array} \right] \in \mathbb{R}^{2N \times 2N} \quad \text{und} \end{split}\]

\[\begin{split}S = \left[ \begin{array}{rrrrrrr} 2 & 0 & -1 & 0 & \cdots & \cdots & 0 \\ 0 & 2 & 0 & -1 & \ddots & & \vdots \\ -1 & 0 & 2 & 0 & \ddots & \ddots & \vdots \\ 0 & -1 & 0 & 2 & \ddots & \ddots & 0 \\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & -1 \\ \vdots & & \ddots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & 0 & -1 & 0 & 2 \end{array} \right] \in \mathbb{R}^{2N \times 2N}.\end{split}\]

\(M\) ist die Massematrix, \(K = k \cdot S\) die Steifigkeitsmatrix und \(D=d \cdot S\) die Dämpfungsmatrix des gekoppelten Systems. Die oben bereits hergeleiteten Bewegungsgleichungen nehmen die bekannte Form eines gedämpften, angetriebenen harmonischen Oszillators

\[M \ddot{\mathbf{z}} + D\dot{\mathbf{z}} + K \mathbf{z} = \mathbf{F}_{\text{ext}}\]

an, nur dass die Koeffizienten \(M, D\) und \(K\) nun matrixwertig sind und die unbekannte Verschiebungsfunktion \(\mathbf{z}(t)\) vektorwertig mit \(2N\) Einträgen ist: Ein Eintrag pro Raumrichtung und beweglichem Massepunkt der Highline.

Ein stationärer Lastfall

Es soll zunächst der stationäre Lastfall untersucht werden, bei dem nur die Schwerkraft auf die Highline wirkt, d.h. Sie gehen von einer konstanten Kraft \(\mathbf{F}_{i,\text{ext}}=\begin{bmatrix} 0 \\ -m g \end{bmatrix}\) mit \(g=9.81\;\textrm{m}/\textrm{s}^2\) sowie \(\ddot{\mathbf{z}}=\dot{\mathbf{z}}=0\) aus. Dies entspricht dem Zustand, der sich nach langer Zeit aufgrund der Dämpfung einstellt. Die Differentialgleichung vereinfacht sich in diesem Fall zu einem linearen Gleichungssystem

\[K \mathbf{z} = \mathbf{F}_{\text{ext}}.\]

Bei einer Highlinelänge von \(L=50\;\textrm{m}\), einem Gesamtgewicht von \(m_{\text{ges}}=3.15\;\textrm{kg}\), sowie einer Gesamtsteifigkeit von \(k_{\text{ges}}=145.5\;\textrm{N}/\textrm{m}\) ergeben sich für die Einzelmassen und Einzelsteifigkeiten

\[ m = \frac{m_{\text{ges}}}{N} \quad \text{ und } \quad k = N \cdot k_{\text{ges}}.\]

Mit \(\mathbf{b} = \left[ \begin{array}{ccccccc} 0 & 1 & 0 & 1 & \cdots & 0 & 1 \end{array} \right]^T \in \mathbb{R}^{2N}\) lässt sich das lineare Gleichungssystem schreiben als

\[\begin{split} \begin{align} &K \mathbf{z} = \mathbf{F}_{\text{ext}} \notag \\ \Leftrightarrow \quad&k \cdot S \mathbf{z} = -m \cdot g \cdot \mathbf{b} \notag \\ \Leftrightarrow \quad&N \cdot k_{\text{ges}} S \mathbf{z} = - \frac{m_{\text{ges}}\cdot g}{N} \mathbf{b} \notag \\ \Leftrightarrow \quad&S \underbrace{\left( - \frac{N^2 \cdot k_{\text{ges}}}{m_{\text{ges}}\cdot g} \mathbf{z}\right)}_{:= \tilde{\mathbf{z}}} = \mathbf{b} \notag \end{align} \end{split}\]

Demnach lassen sich die Verschiebungen der Massepunkte im stationären Lastfall berechnen, indem das lineare Gleichungssytem

\[S \tilde{\mathbf{z}} =\mathbf{b}\]

gelöst wird. Die Verschiebungen \(\mathbf{z}\) erhält man aus der entdimensionalisierten Lösung \(\tilde{\mathbf{z}}\) des Gleichunssystemes mittels

\[\mathbf{z} = - \frac{m_{\text{ges}}\cdot g}{N^2 \cdot k_{\text{ges}}} \tilde{\mathbf{z}}.\]

Aufgabe 1 - Durchhang der Highline ohne Zusatzgewicht

Lösen Sie das Gleichungssystem \(S \tilde{\mathbf{z}} = \mathbf{b}\) mit \(S \in \mathbb{R}^{2N \times 2N}\) und \(\mathbf{b} \in \mathbb{R}^{2N}\) für verschiedene Werte für \(N\) mit Hilfe des Backslash-Operators S\b und berechnen Sie anschließend die Verschiebung der Massepunkte \(\mathbf{z}\). Erzeugen Sie \(S\) dazu im Sparse-Matrix-Format, wie in der vorherigen Übung beschrieben.

Hinweis

Klappen Sie die Codebox aus, um auf den Code für plot_highline zuzugreifen. Wenn Sie Ihren Code online ausführen, brauchen Sie die Funktion nicht initialisieren, da sie dem Kernel als Datei hinterlegt ist.

Show code cell source Hide code cell source

function handle = plot_highline(z, L)
    % plots the highline according to the (x,y)-coordinates stored in the flat
    % vector z = [x1,y1, x2, y2, x3, y3, ...] and the length L of the highline.

    N = length(z)/2;

    if N - floor(N) > 1e-15
        error("The length of the input vector z must be divisble by 2!");
    end

    positions_x = z(1:2:end)' + L*linspace(1/(N+1), 1 - 1/(N+1), N);
    positions_y = z(2:2:end)';

    positions_x = [0 positions_x L];
    positions_y = [0 positions_y 0];

    handle = plot(positions_x, positions_y);

    xlabel('x [m]')
    ylabel('y [m]')
    title('highline displacement')

end

% space for the solution

% S = ...
% b = ...


% z = ...

% plot the displacement of the slackline based on the solution vector z as well as the length of the slackline L
% (the function plot_highline is provided for you, you do not need to implement this)
plot_highline(z, L)

% uncomment the following line to have equal spacing along the x- and y-axis
%axis equal

• Wie stark hängt die Highline an der tiefsten Stelle durch?

• Wie hoch muss die Auflösung \(N\) Ihrer Ansicht nach mindestens sein, um dem Ergebnis vertrauen zu können? Begründen Sie Ihre Antwort mit konkreten Zahlen!

Aufgabe 2 - Vergleich iterativer Gleichungssystemlöser

Ab einer bestimmten Größe des Gleichungssystems sind iterative Verfahren zum Lösen von linearen Gleichungssystem besser geeignet als direkte Lösungsverfahren wie das LU-Verfahren.

Prominente Vertreter iterativer Verfahren für lineare Gleichungssysteme sind das konjugierte Gradientenverfahren (Matlab: cgs), das Minres-Verfahren (Matlab: minres) sowie das BiCGstab-Verfahren (Matlab: bicgstab).

Die Konvergenzgeschwindigkeit der iterativen Verfahren lässt sich durch Vorkonditionierung, z.B. mittels unvollständiger LU-Zerlegung, verbessern. Für das BiCGstab-Verfahren sieht der Befehl so aus:

% construct preconditioner 
option.thresh = 0.01;
[L,U,P] = ilu(S,option);

% calculate solution using preconditioned bicgstab
zt = bicgstab(S,P*b,[],maxit,L,U);

Vergleichen Sie die zur Lösung des linearen Gleichungssystems \( S\tilde{\mathbf{z}} =\mathbf{b}\) benötigte Rechenzeit des klassischen LU-Verfahrens

[L, U, P] = lu(S);
y  = L\P*b;
zt = U\y; 

mit denen der drei iterativen Verfahren, jeweils mit und ohne Vorkonditionierung und für unterschiedliche \(N\). Verwenden Sie das Speicherformat für dünnbesetzte Matrizen. Erstellen Sie zwei Tabellen, in denen Sie jeweils die benötigte Rechenzeit bzw. das Residuum res = max(abs(b-S*zt)) eintragen:

Verfahren/N	5	50	500	…
LU	…	…	…	…
cgs	…	…	…	…
minres	…	…	…	…
bicgstab	…	…	…	…
prec. cgs	…	…	…	…
prec. minres	…	…	…	…
prec. bicgstab	…	…	…	…

• Ab welcher Auflösung \(N\) ist das Schnellste der sechs iterativen Verfahren schneller als das klassische LU-Verfahren?

Tipp

• Verwenden Sie die Matlabbefehle tic und toc für die Zeitmessung.

• Unter Umständen müssen Sie die maximal erlaubte Anzahl an Iterationen für die iterativen Verfahren anpassen.

• Denken Sie daran, die Konstruktion des Vorkonditionierers in der Rechenzeit zu berücksichtigen!

% space for the solution

Aufgabe 3 - Simulation der Slacklinerin

In einer sogenannten quasistatischen Simulation wird ein zeitabhängiger Prozess so simuliert, dass in jedem Zeitschritt ein stationärer Zustand berechnet wird. So wird die Dynamik (z.B. Oszillation der Slackline) vernachlässigt, was die Berechnung deutlich vereinfacht. Schließlich muss keine Differentialgleichung gelöst werden, es reicht eine Abfolge von linearen Gleichungssystemen zu lösen.

Abbildung 2: Animation der Slacklinerin und des Durchhangs des Seils beim Überqueren der Highline.

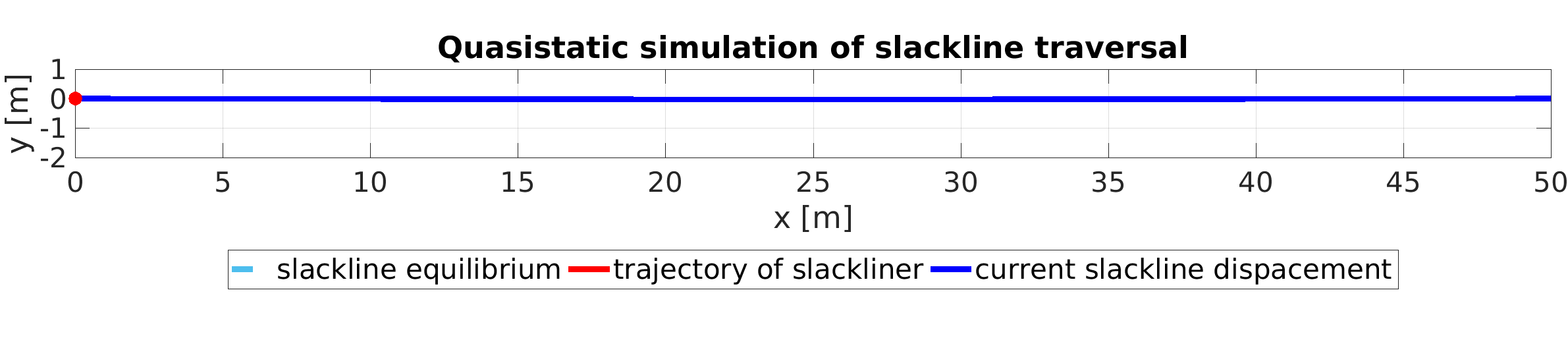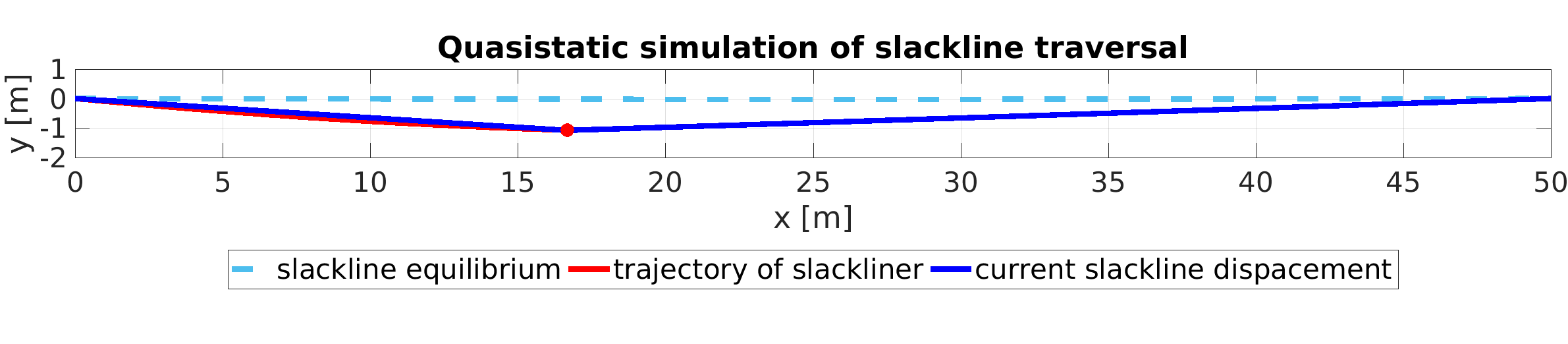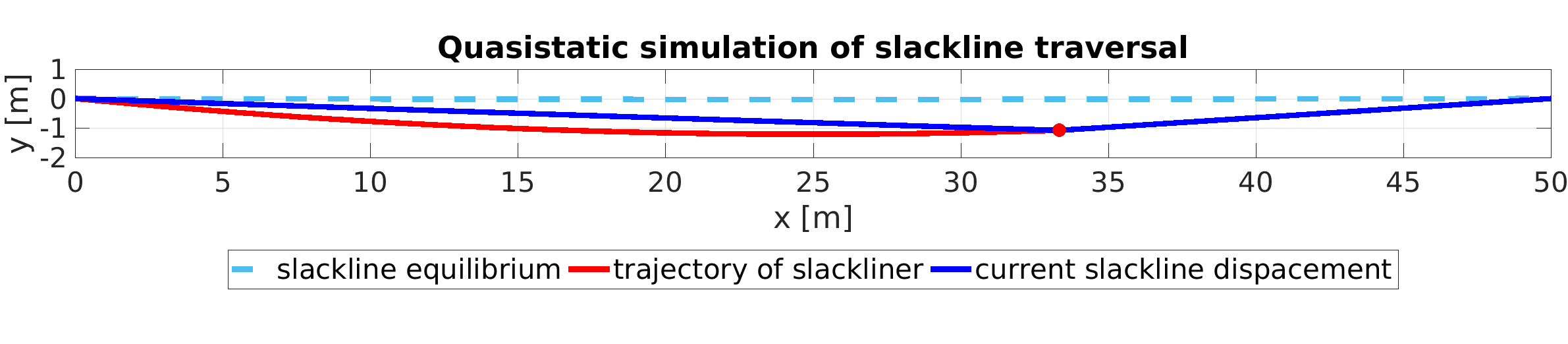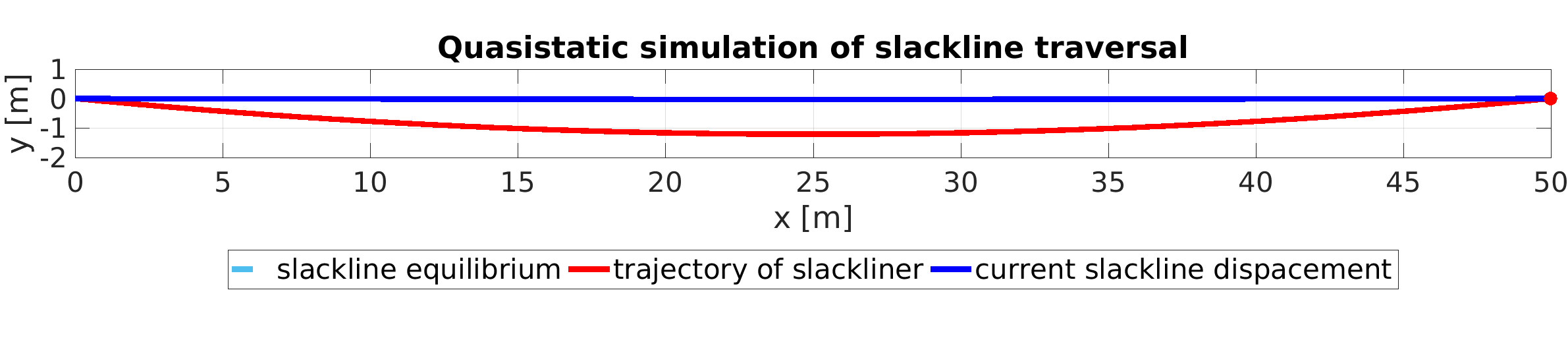
Simulieren Sie, wie eine Slacklinerin die Highline von links nach rechts traversiert. Berechnen Sie dazu die statische Verschiebung der Slackline für unterschiedliche Positionen der Slacklinerin entlang der Highline. Gehen Sie von einem Gewicht von 70 kg aus.

• Treffen Sie eine angemessene Wahl für

  • die räumliche Diskretisierung \(N\) der Slackline, sowie der Schrittweite der Slacklinerin;

  • das Lösungsverfahren für das lineare Gleichungssystem;

  • das Speicherformat der Matrix

  und begründen Sie Ihre Antwort.

• Plotten Sie die Kurve, die von den Füßen der Slacklinerin durchlaufen wird (Rote Linie in der Animation in Abbildung 2). Wie stark hängt die Slackline am tiefsten Punkt durch?

% space for the solution

Es geht weiter mit der Highline

Um die Highline dynamisch zu simulieren, sehen Sie sich die Übung Modellierung einer Highline - Zeitliche Auflösung an.