Voraussetzungen
mathematische Grundlagen der Spline Interpolation
Lerninhalte
Anwendung der Spline Interpolation
Spline-Interpolation#
Im Handwerk ist die Straklatte (engl.: Spline) ein zentrales Werkzeug für das Entwerfen von Geometrien. Der große Vorteil ist, dass allein durch die Definition einzelner Punkte eine durchgängige Geometrie definiert werden kann, die keine Kanten enthält. Diese kann einfach reproduziert werden, indem die Punkte wieder aufgezeichnet werden und eine ähnliche Latte (dabei ist in erster Linie die Länge entscheidend) um die Punkte gelegt wird. Siehe Wikipedia für eine bildliche Darstellung.
Auch in CAD Standards wie STEP (.stp Dateien) wird diese Methode verwendet, um digitale Geometrien zu definieren, siehe hier.
Sie erhalten nun für Ihre Linie die folgenden Punkte (siehe Abbildung):
\(x [cm]\) |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
|---|---|---|---|---|---|---|
\(y [cm]\) |
0.0 |
1.0 |
0.8 |
1.8 |
1.6 |
2.4 |
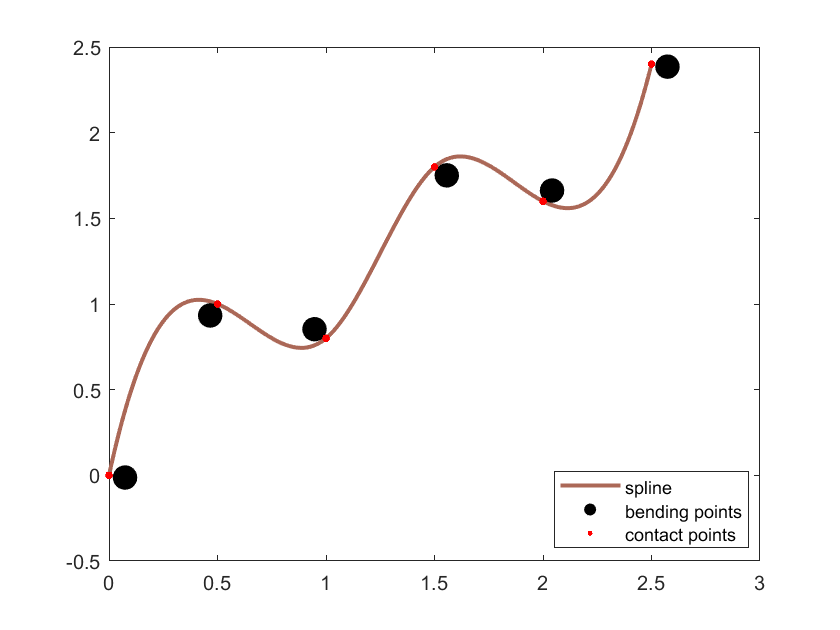
Abbildung 1: Verlauf der Straklatte (braun) um die angegebenen Punkte (schwarz) mit Kontaktpunkten (rot). Hier wurden Polynome dritten Grades verwendet.
Diese Punkte sollen nun interpoliert werden, um möglichst genaue Werte über den gesamten Verlauf zu erhalten (Verwenden Sie hierbei keine fertige Matlab Spline-Funktion - Finger weg von der Spline-Toolbox!). Dazu wird jedes Teilintervall mit einem geeigneten Polynom genähert.
Aufgabe 1#
Konstruieren Sie eine quadratische Splinefunktion durch die ersten drei Punkte mit Bleistift und Papier. Bestimmen Sie die Koeffizienten der gesuchten Funktionen \(y_i(x) = a_i + b_i(x-x_i) + c_i(x-x_i)^2, i \in [1,n_\text{Punkte}-1]\).
Hinweis
Zur eindeutigen Bestimmung der einzelnen Polynome sind drei Bedingungen notwendig. Zwei sind durch den Anfangs- und Endpunkt des jeweiligen Intervalls gegeben. Um Knicke in der gesamten Spline zu vermeiden wird zusätzlich gefordert, dass die ersten Ableitungen an den Intervallgrenzen übereinstimmen (dritte Bedingung). Welche Randbedingung ist für die erste Ableitung an der Einspannung zu wählen?
Aufgabe 2#
Implementieren Sie eine Matlab-Funktion
function yfine = quadraticSpline(x, y, xfine, bc), die für gegebene x- und y-Werte sowie Randbedingung an den vonxfinedefinierten Punkten die entsprechenden y-Werte des Splines berechnet.
%%file quadraticSpline.m
function yfine = quadraticSpline(x, y, xfine, bc)
% yfine = quadraticSpline(x, y, xfine, bc) calculates the quadratic spline going through the
% points defined by xi and yi and evaluates the spline at the points in xfine.
...
end
Testen Sie die Funktionalität mit der bereitgestellten Test Suite
test_quadraticSpline.m, siehe unten. Es reicht zunächst, dass die ersten fünf der Unit Tests erfolgreich sind. Challenge: Schaffen Sie es, alle neun Unit Tests zu erfüllen?
% test the quadraticSpline function
moxunit_runtests test_quadraticSpline.m
Nun soll der Spline Verlauf mit einer Schrittweite von 1 mm interpoliert werden. Erstellen Sie dazu ein Skript, in welchem Ihre Funktion auf die obigen Messwerte angewandt wird. Stellen Sie die interpolierte Spline in einem Plot dar.
%script to apply function to the given values
%uncomment to equalize axis:
%axis equal
Aufgabe 3 (Zusatzaufgabe):#
Nutzen Sie Ihren Code aus Aufgabe 2 um eine Funktion
yfine = cubicSpline(x,y,xfine,bc)zu erstellen.Nutzen Sie die
SplineFunktion von Matlab, um eigene Unit Tests für IhrecubicSplinefunktion zu schreiben (einfache Vergleiche für einige Test-Sets an Punkten genügen).
%%file cubicSpline.m
function yfine = cubicSpline(x,y,xfine,bc)
...
end
%%file test_cubicSpline.m
%unit tests using Spline
% test the quadraticSpline function
% test the cubicSpline function
moxunit_runtests test_cubicSpline.m

