Game of Life

Game of Life#

Conway’s Game of Life (dt. Spiel des Lebens) wurde 1970 von dem Mathematiker John Horton Conway entwickelt und basiert auf einem zweidimensionalen zellulären Automaten.

Das Spielfeld#

Das Spielfeld besteht aus Feldern, die schachbrettartig in Zeilen und Spalten angeordnet sind und ist im Idealfall unendlich groß. Jedes Feld stellt einen zellulären Automaten dar und wird hier auch Zelle genannt.

Zellen können einen von zwei Zuständen annehmen. Diese werden oft ‘lebendig’ bzw. ‘tot’ genannt.

Beim Spielen des Spiels wird zunächst eine (zufällige) Anfangsgeneration von lebenden Zellen auf dem Spielfeld platziert. Jede Zelle hat genau acht Nachbarzellen, die zur Bestimmung der Folgegeneration berücksichtigt werden müssen. Die nächste Generation ergibt sich durch die Befolgung einfacher Regeln.

Abbildung 1: Beispiel für einen Game of Life Durchlauf mit zufälliger Startverteilung und n = 100 Iterationen.

Das Spiel des Lebens kann mit Hilfe eines Computers simuliert (= gespielt) werden. Da in diesem Fall das Spielfeld immer endlich ist, muss es einen Rand haben, an dem die Regeln gesondert festgelegt werden müssen. Eine Möglichkeit ist, dass der Rand komplett durch tote/lebendige Zellen belegt ist. Eine Alternative sind sogenannte periodische Randbedingungen, bei denen alles, was das Spielfeld nach unten verlässt, oben wieder hereinkommt und umgekehrt bzw. alles, was das Spielfeld nach links verlässt, rechts wieder eintritt und umgekehrt.

Die Spielregeln#

Die Folgegeneration wird für alle Zellen gleichzeitig berechnet und ersetzt die aktuelle Generation. Der Zustand einer Zelle (lebendig oder tot) in der Folgegeneration hängt nur vom aktuellen Zustand der Zelle selbst und den aktuellen Zuständen ihrer acht Nachbarzellen ab.

Die von Conway ursprünglich verwendeten Regeln sind:

Eine tote Zelle mit genau drei lebenden Nachbarn wird in der Folgegeneration neu geboren
Lebende Zellen mit weniger als zwei lebenden Nachbarn sterben in der Folgegeneration an Einsamkeit
Eine lebende Zelle mit zwei oder drei lebenden Nachbarn bleibt in der Folgegeneration am Leben
Lebende Zellen mit mehr als drei lebenden Nachbarn sterben in der Folgegeneration an Überbevölkerung

Aufgabe 1#

Schreiben Sie einen Matlab Code, der ein quadratisches Spielfeld der Größe N x N anlegt. Implementieren Sie je eine Auswahl für verschiedene Anfangsgenerationen (siehe 1.2) bzw. verschiedene Spielfeldränder (siehe 1.3).

1.1 Spielfeld#

Legen Sie fest, welche Größe Ihr quadratisches Spielfeld haben soll.

N = 10; % Größe des Spielfelds

1.2 Anfangsgeneration#

Ermöglichen Sie eine Auswahl verschiedener Anfangsgenerationen:

Eine zufällige Verteilung von toten und lebendigen Zellen

% entweder Zufallsverteilung:
% erzeugt ein quadratisches array der Größe (N x N) mit ganzzahligen Zufallswerten zwischen 0 und 1
field = randi([0, 1], [N, N]); 

Ein R-Pentomino in der Mitte des Spielfelds (siehe Abbildung 2). Hier soll die minimale Spielfeldgröße N=10 betragen, selbst wenn N vorher kleiner gewählt wurde.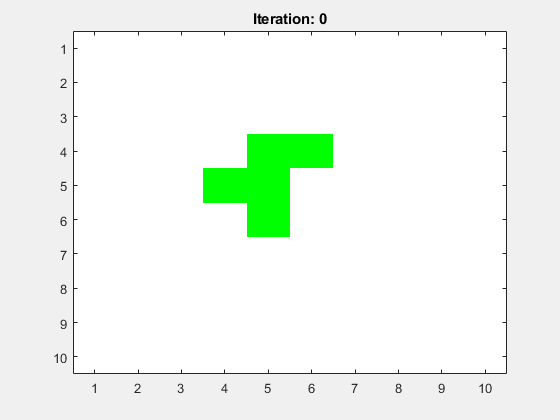

Abbildung 2: Ein R-Pentomino in der Mitte des Spielfelds. Alle anderen Zellen haben hier den toten Zustand.

% R-Pentomino:
field = R_pentomino(N);

function field = R_pentomino(N)
    if N < 10
        N = 10;
    end
    
    field = zeros(N, N);
    mid = round(N/2);
    field(mid-1, mid:mid+1) = 1;
    ...
    return
end

Einen Glider in der Mitte des Spielfelds (siehe Abbildung 3). Auch hier soll die minimale Spielfeldgröße N=10 betragen, selbst wenn N vorher kleiner gewählt wurde.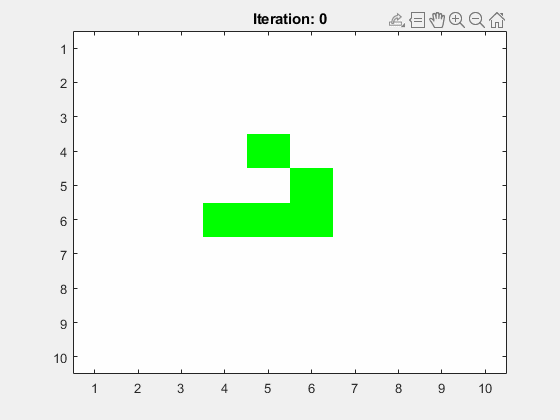

Abbildung 3: Ein Glider in der Mitte des Spielfelds. Alle anderen Zellen haben hier den toten Zustand.

% Glider:
field = Glider(N);

function field = Glider(N)
    if N < 10
        N = 10;
    end
    
    ...
end

Ein Light Weight Spaceship (LWSS), Medium Weight Spaceship (MWSS) bzw. Heavy Weight Spaceship (HWSS) in der Mitte des Spielfelds (siehe Abbildunen 4-6). Hier soll die minimale Spielfeldgröße N=20 betragen, selbst wenn N vorher kleiner gewählt wurde.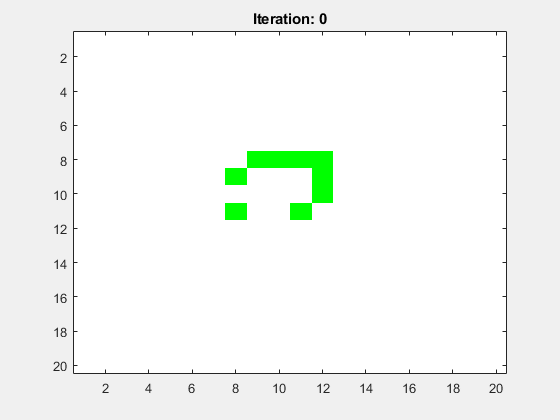

Abbildung 4: Ein Light Weigth Spaceship (LWSS) in der Mitte des Spielfelds. Alle anderen Zellen haben hier den toten Zustand.

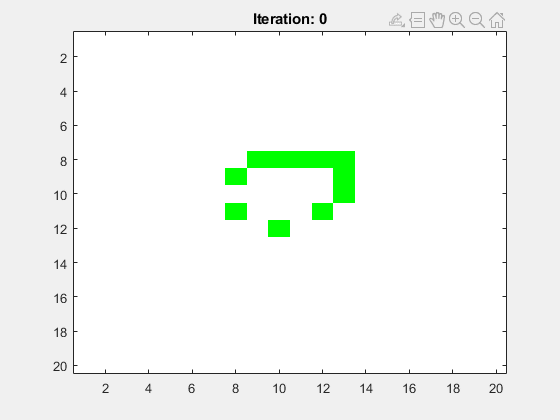Abbildung 5: Ein Medium Weigth Spaceship (MWSS) in der Mitte des Spielfelds. Alle anderen Zellen haben hier den toten Zustand.

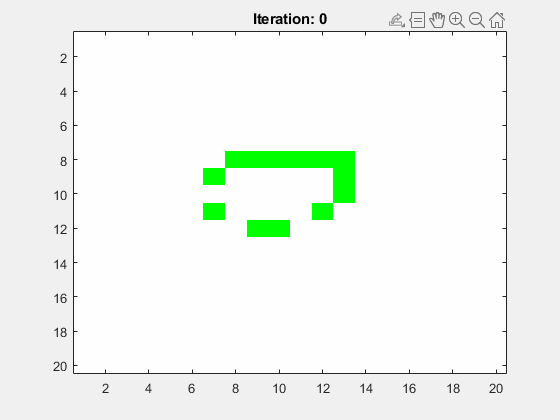Abbildung 6: Ein Heavy Weigth Spaceship (HWSS) in der Mitte des Spielfelds. Alle anderen Zellen haben hier den toten Zustand.

% Spaceships
field = LWSS(N);

function field = LWSS(N)
    if N < 20
        N = 20;
    end
    
    ...
end

function field = MWSS(N)
    ...
end

function field = HWSS(N)
    ...
end

1.3 Spielfeldrand#

Realisieren Sie folgende Spielfeldränder, von denen immer genau eins ausgewählt sein soll:

Alle äußeren Zellen sind immer tot (rule 1)
Alle äußeren Zellen sind immer lebendig (rule 2)
Periodisches Spielfeld (siehe Abb. 7): Was links/rechts/oben/unten das Spielfeld verlässt kommt auf der gegenüberliegenden Seite wieder rein (rule 3)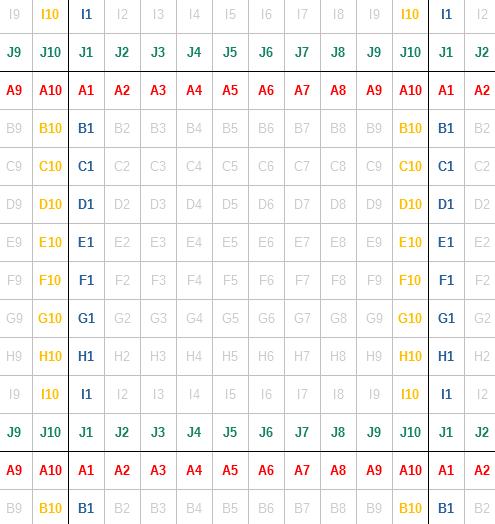

Abbildung 7: Beispiel für periodische Randbedingungen. Das Spielfelds wird oben/unten bzw. links/rechts an sich selbst kopiert. Etwas das z.B. rechts das Spielfeld verlassen würde kommt so auf der linken Seite wieder rein.

rule = 1; % only dead cells
% or
%rule = 2; % only living cells
% or
%rule = 3; % PBC

field = add_boundaries(field, rule, N);

function field = add_boundaries(field, rule, N)
% add field boundaries based on selected rule
    if rule == 1
    % boundaries are only dead cells (0)
        top_bottom = zeros(1, N+2);
        sides = zeros(N, 1);
        
        field = [top_bottom;
                 sides field sides;
                 top_bottom];
                 
    elseif rule == 2
    % boundaries are only living cells (1)
        ...
    elseif rule == 3
    % periodic boundary conditions (PBC)
        ...
    else
    % rule is neither equal to 1, 2 or 3
        ...
    return
end

1.4 Visualisierung#

Lassen Sie sich die Startverteilung visuell darstellen.

figure; hAxes = gca;
imagesc(hAxes, field(2:end-1, 2:end-1)); % Der Rand, der über add_boundaries hinzugefügt wird, wird hier nicht mit anzeigt
colormap(hAxes , [1 1 1; 0 1 0]);
hold on
pause(0.5)

Aufgabe 2#

Erweitern Sie Ihren Matlab Code nun so, dass für eine vorherbestimmte Anzahl an Iterationen jeweils die Folgegeneration bestimmt und anschließen angezeigt wird.

Probieren Sie die verschiendenen Startverteilungen und Randbedingungen aus (vgl. Abb. 8-10).

Iterations = 100; %Anzahl an Spielrunden

for i=1:Iterations
    field = next_iteration(field, N)
    
    %plot
    imagesc(hAxes, field(2:end-1, 2:end-1));
    colormap(hAxes, [1 1 1; 0 1 0]);
    hold on
    
    pause(0.1)
end

function field = next_iteration(field, N, rule)
    new_field = zeros(N,N);    
    % current field size (N+2)x(N+2) because boundaries were added previously
    for i=2:N+1
        for j=2:N+1
            count = count_living_cells(field,i,j);             

            % take aktion based on living or dead cell
            new_field(i-1,j-1) = update_cell(field(i,j), count);                
        end
    end
    
    % add boundaries to the new field
    new_field = add_boundaries(new_field, rule, N);

    % make new_field the current field
    field = new_field;
    return
end

function count = count_living_cells(field, i, j)
    count = 0;
    % check number living neighbour cells
    % add above the cell
    count = count + sum(field(i-1,j-1:j+1));
    % add below the cell
    count = count + sum();
    % add left side
    ...
    return
end

function val = update_cell(cell, count)
    if cell == 1
        % living cell
        % if less than to living neighbours: cell dies
        if count < 2
            val = 0;
        elseif count <= 3
            % if 2 or 3 living neighbour cells: cell stays alive
            val = ...;
        else
            % if more than 3 living neighbour cells: cell dies due
            % to overpopulatoin
            ...
        end
    else
        % dead cell
        ...
    end
    return
end

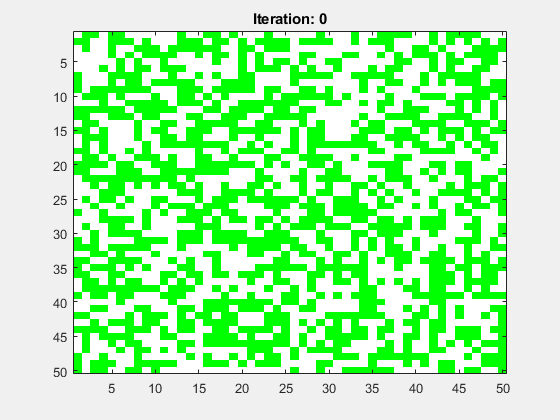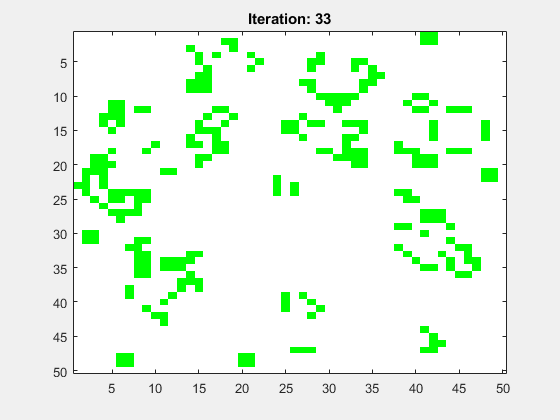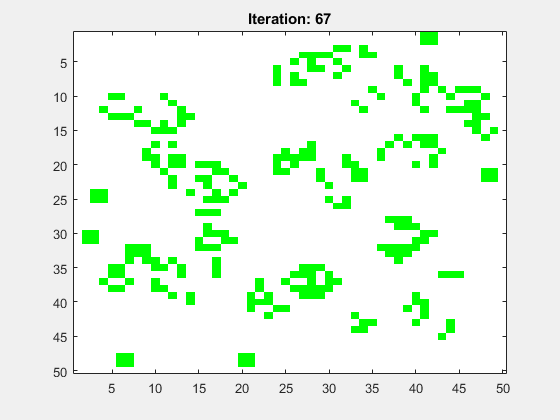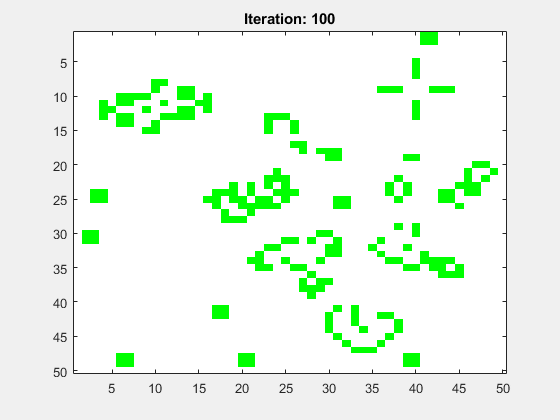
Abbildung 8 zeigt die Animation für ein mittig platziertes R-Pentomino. Das Spielfeld hat die Größe N=50 und die Anzahl der Folgegenerationen ist Iterations=100. Als Randbedinung wurde festgelegt, dass alle Zellen dort tot sind.

Abbildung 8: Ein R-Pentomino in der Mitte eines 50x50 Spielfelds und 100 Folgegenerationen mit einem Rand auf dem alle Zellen tot sind.

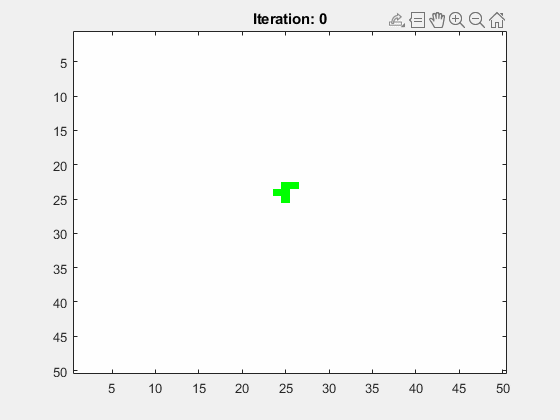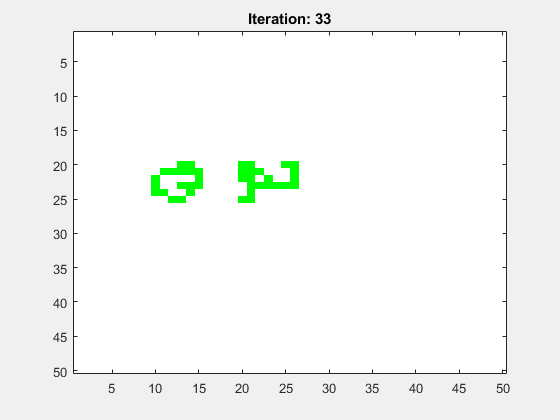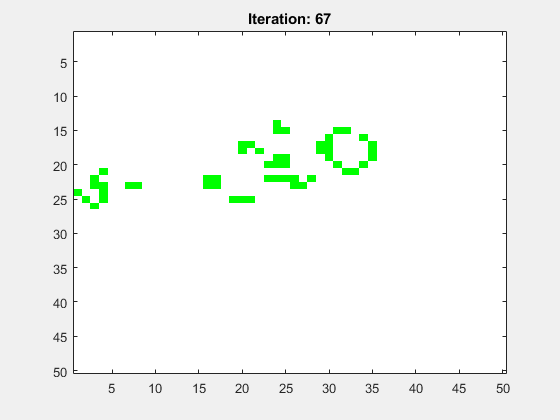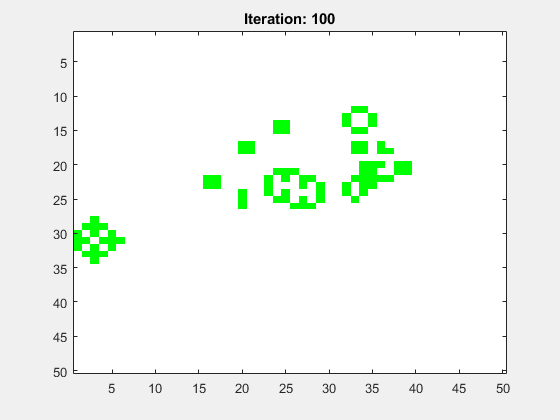
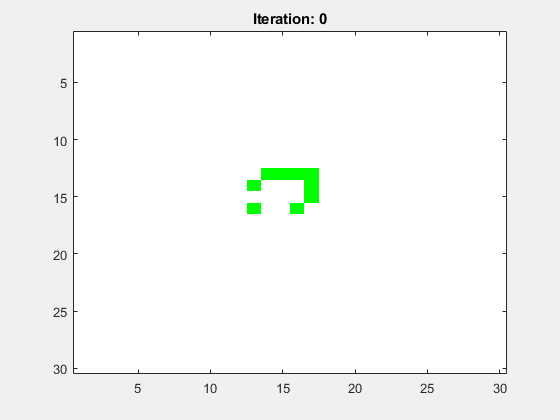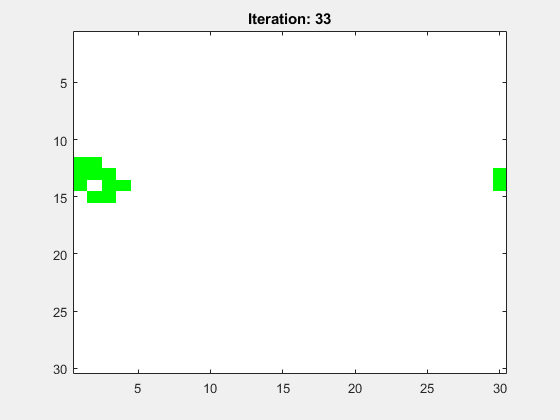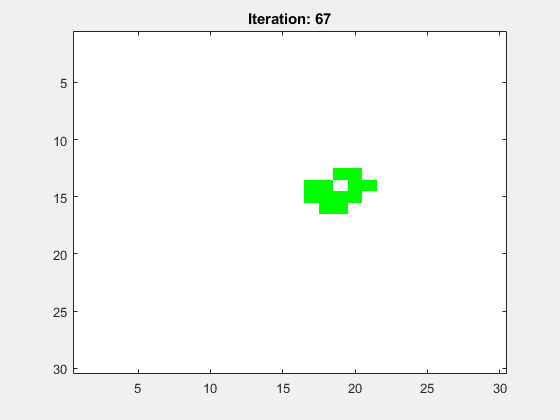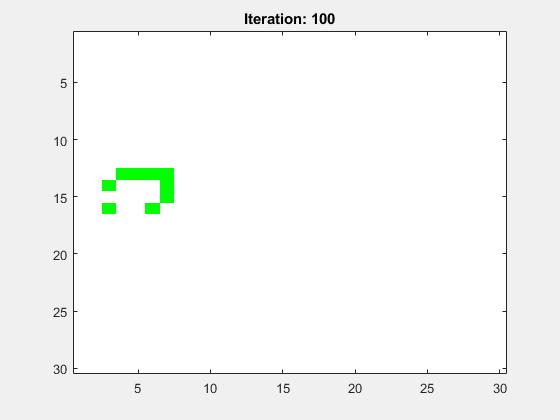
Abbildung 9 zeigt die Animation für ein mittig platzierten Glider. Das Spielfeld hat die Größe N=30 und die Anzahl der Folgegenerationen ist Iterations=100. Es wurden periodische Randbedingungen (periodic boundary conditions, PBC) gewählt.

Abbildung 9: Ein Glider in der Mitte eines 30x30 Spielfelds und 100 Folgegenerationen mit PBC.

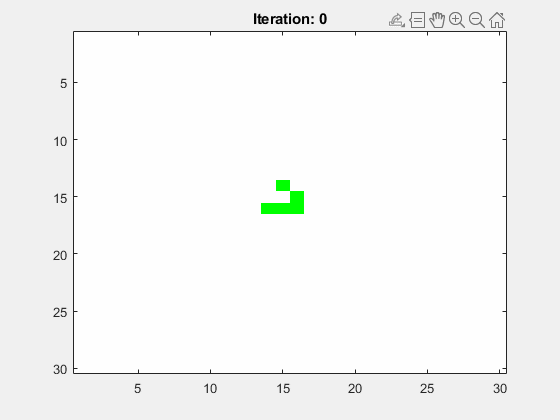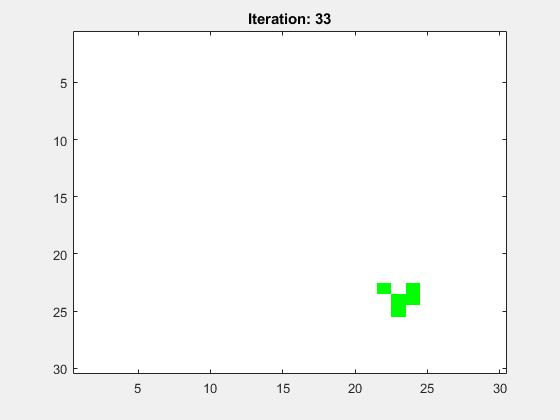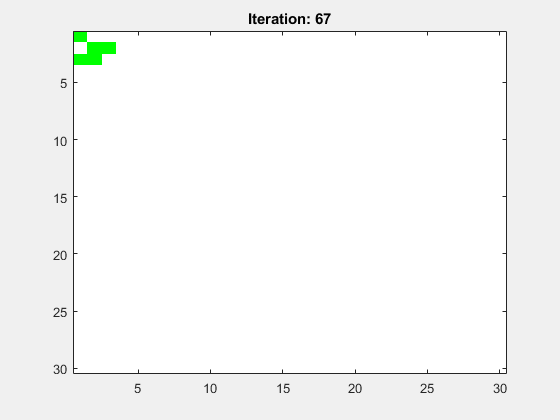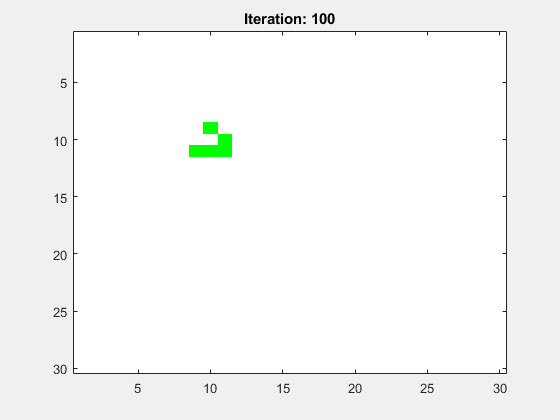
Abbildung 10 zeigt die Animation für ein mittig platziertes Light Weight Spaceship (LWSS). Das Spielfeld hat die Größe N=30 und die Anzahl der Folgegenerationen ist Iterations=100. Es wurden periodische Randbedingungen (periodic boundary conditions, PBC) gewählt.

Abbildung 10: Ein LWSSin der Mitte eines 30x30 Spielfelds und 100 Folgegenerationen mit PBC.