Ctrl+K

Approximation von periodischen Signalen

Voraussetzungen

  • mathematische Grundlagen der Fouriertransformation

Lerninhalte

  • Implementierung einer diskreten Fouriertransformation

Approximation von periodischen Signalen#

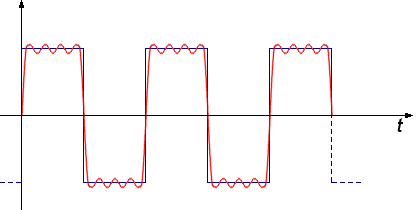
Aufgabe 1: Rechteckssignal#

Entwickeln Sie eine Matlab/Octave-Funktion, mit deren Hilfe Sie ein Rechtecksignal mit vorgegebener Frequenz freq durch Überlagerung von Sinus- und Kosinusfunktionen erzeugen können. Da Sie die dafür nötige Reihe nicht unendlich genau berechnen können, muss dabei die maximal auftretende Frequenz der verwendeten harmonischen Schwingungen \(f_{max}\) beschränkt werden.

Verwenden Sie nicht die fft Funktion. Berechnen Sie die Koeffizienten von Hand vor.

../_images/rechteckSignal.png 
%%file fourier_approx_rectangular.m
function a = fourier_approx_rectangular(amplitude, freq, f_max)
% calculates the complex Fourier coefficients of a periodic rectangular signal.
%
% amplitude denotes the amplitude of the input signal [unit implied]
% freq denotes the frequency of the input signal [Hz]
% f_max denotes the highest frequency to be used for the approximation [Hz]
% 
%  INSERT CODE HERE
%

Betrachten Sie dann eine Periode des so erzeugten Signals und lösen diese mit 1000 Punkten auf. Wie groß ist für eine gegebene Amplitude und Frequenz die betraglich größte Abweichung für \(f_{max}=10\) Hz, \(f_{max} = 50\) Hz, \(f_{max}=200\) Hz?

% SPACE FOR SOLUTION

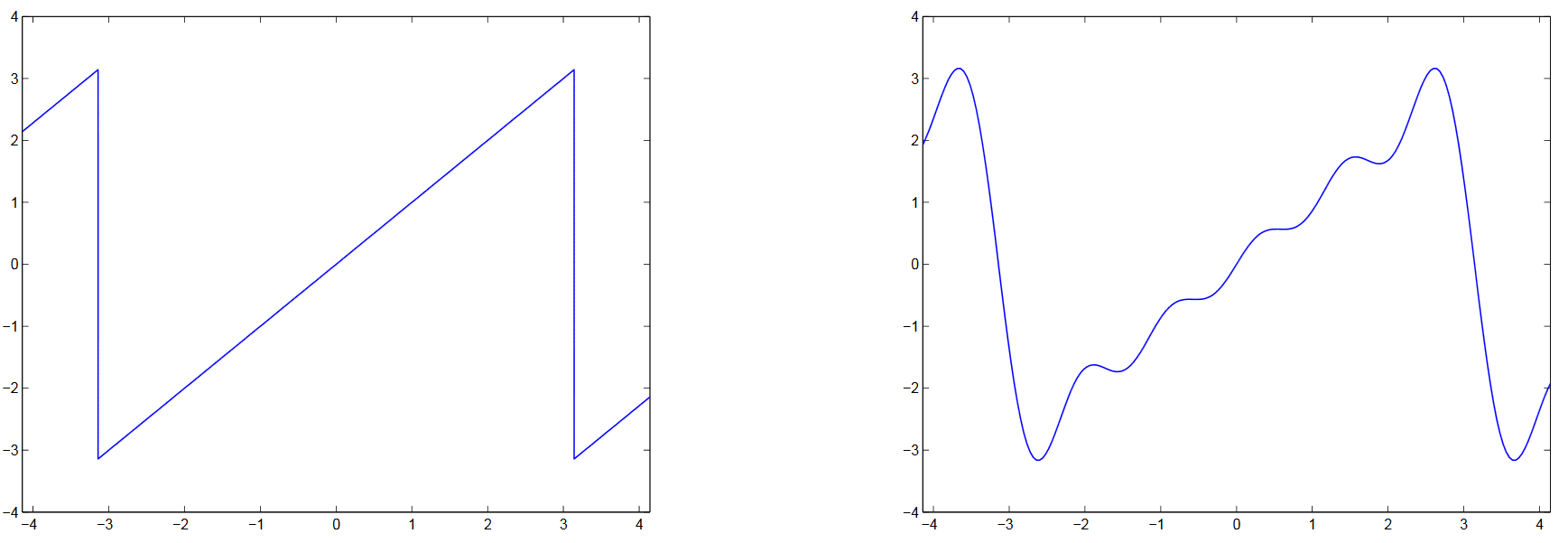
Aufgabe 2: Sägezahnfunktion#

Wiederholen Sie Aufgabe 1 für die Sägezahnfunktion

\[ s(t) = 2Aft, \:\:\:\: t \in \left[-\frac{T}{2}, \frac{T}{2}\:\right) \]

mit Amplitude \(A\) und Frequenz \(f=\frac{1}{T}\).

../_images/saegezahn.png 
%%file fourier_approx_rectangular.m
function a = fourier_approx_sawtooth(amplitude, freq, f_max)
% calculates the complex Fourier coefficients of a periodic sawtooth signal.
%
% amplitude denotes the amplitude of the input signal [unit implied]
% freq denotes the frequency of the input signal [Hz]
% f_max denotes the highest frequency to be used for the approximation [Hz]
% 
%  INSERT CODE HERE
%

Betrachten Sie dann eine Periode des so erzeugten Signals und lösen diese mit 1000 Punkten auf. Wie groß ist für eine gegebene Amplitude und Frequenz die betraglich größte Abweichung für \(f_{max}=10\) Hz, \(f_{max} = 50\) Hz, \(f_{max}=200\) Hz?

% SPACE FOR SOLUTION
Contents