Voraussetzungen
Programmier-Grundlagen
dynamische Kräftegleichgewichte
Lerninhalte
Lösung und graphische Darstellung der harmonischen Schwingungsgleichung als ODE
Harmonische Schwingung#
Unter einer harmonischen Schwingung versteht man eine Schwingung, die vollständig mit der Sinus- bzw. Kosinusfunktion beschrieben werden kann. Dazu gehört das einfache Fadenpendel, das trotz der starken Vereinfachung eine gute Vorstellung davon gibt, mit welchen mathematischen Problemstellungen Ingenieur:innen in der Praxis oft konfrontiert werden. Häufig haben die Differentialgleichungen eine Lösung der Form
Aufgabe 1: Fadenpendel#
Nutzen Sie Matlab/Octave, um das Verhalten eines Fadenpendels zu simulieren. Stellen Sie dazu zunächst mit Stift und Papier die zu lösende Differentialgleichung auf.
Tipp: Vielleicht hilft Ihnen die Energieerhaltung oder das dynamische Kräftegleichgewicht (D’Alembert) bei der Herleitung!
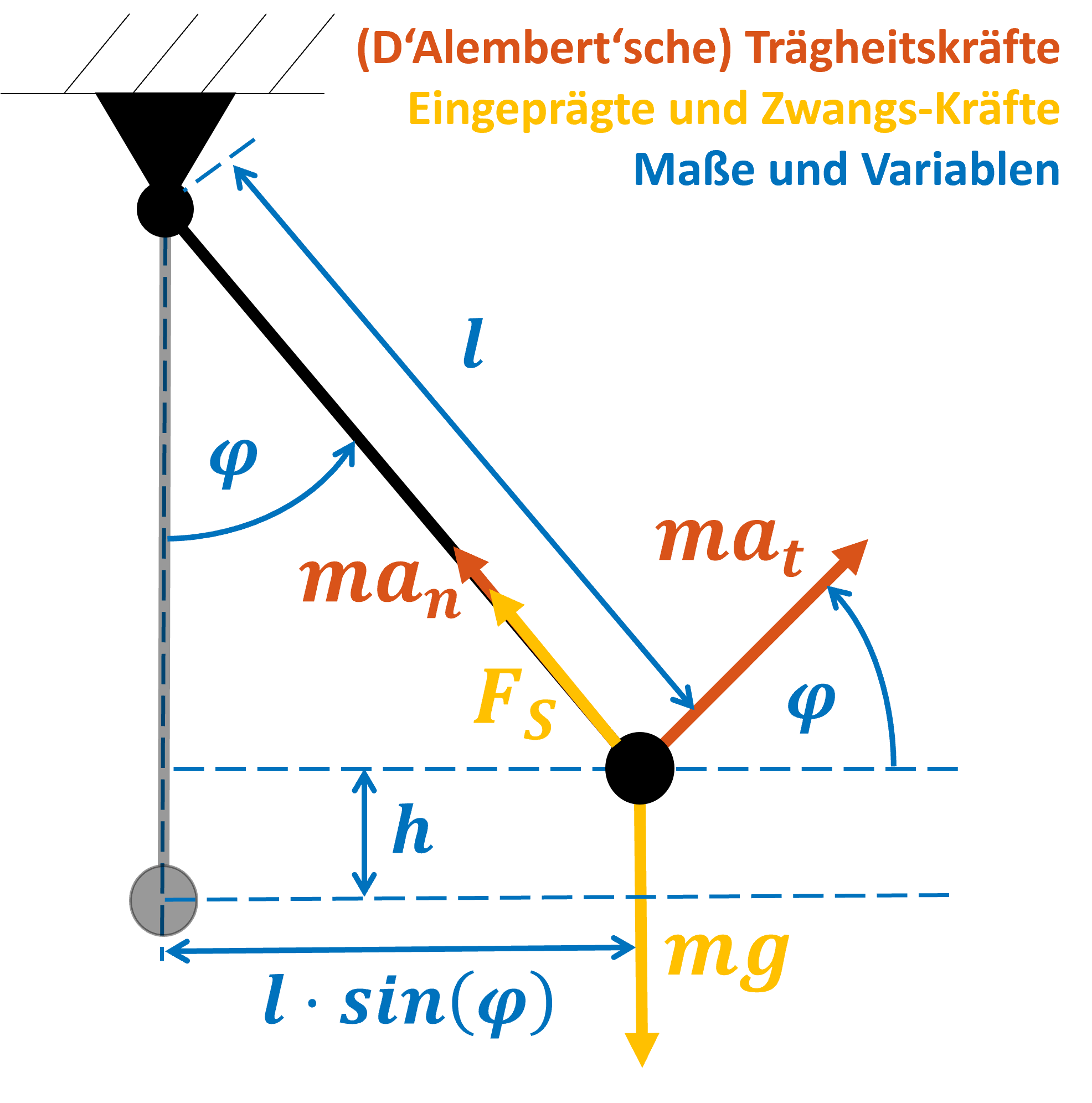
Abbildung 1: Das Pendel als klassisches Schwingungsbeispiel. Eingezeichnet sind die Trägheitskräfte (rot), eingeprägte und Zwangskräfte (gelb) und Maße und Variablen (blau). Das Pendel ist im ausgelenkten (schwarz) und hängenden (grau) Zustand dargestellt.
Nun stehen wir vor der Herausforderung ein zeitkontinuierliches Problem mit unseren endlichen Ressourcen zu lösen! Wie gelingt uns dies? Und wie können wir eine diskrete Zeit in Matlab ausdrücken?
Tipp: Vielleicht kommen wir mit dieser Funktion einen Schritt näher?
Nun können wir unser Problem Matlab/Octave mitteilen. Dazu geben wir zunächst allen Variablen und konstanten Größen einen Wert:
Zu Beginn der Simulation soll das Pendel parallel zum Boden ausgelenkt sein und ruhen.
Die Länge des Seils soll 5m betragen.
Die Simulation beginnt zum Zeitpunkt \(t_0 = 0\).
g = ; %Gravitationskonstante
l = ; %Länge des Seils
x0 = [, ]; %Anfangsbedingung
t_start = ; %Zu welchem Zeitpunkt die Simulation beginnt
t_end = ; %Zu welchem Zeitpunkt die Simulation endet
t_steps = ; %Anzahl der Zeitschritte zwischen t_start und t_end
t_interval = ; %Zeitvektor
Die DGL, die wir zu Beginn aufgestellt haben, können wir nun auch in Vektorform aufschreiben:
dgl = @(t,x) [ ; ]; %Eine Funktion, mit t und x als Variablen
Unser nun diskretes Problem können wir problemlos mit den uns zur Verfügung stehenden Hilfsmitteln lösen. Dazu benötigen wir nichts weiter als Stift und Papier… und eine Menge Geduld, wenn wir eine brauchbare Zeitauflösung verfolgen! Wie können wir unsere nun zeitdiskrete Differentialgleichung mit Hilfe von Matlab/Octave lösen?
Tipp: Hier finden Sie Informationen zur Anwendung einer der populärsten Möglichkeiten unser Problem zu lösen!
[t, x] = ; %Lösung der DGL nach x in Abhängigkeit von t
Plotten Sie nun das Ergebnis. Dazu bietet es sich an, zunächst ein Winkel-Zeit-Diagramm und ein Geschwindigkeits-Zeit-Diagramm auszugeben. Die Lösung unserer Differentialgleichung wurde in \(x\) gespeichert und besteht aus zwei Spalten, dem Winkel und der Geschwindigkeit.
Tipp: Wie man auf einzelne Spalten einer Matrix zugreift und weiteres zur Indizierung von Arrays in Matlab/Octave finden Sie zum Beispiel hier.
phi_t = x( , )'; %Auslesen der Winkel-Komponenten aus dem Ergebnisvektor x
omega_t = x( , )'; %Auslesen der Winkelgeschwindigkeits-Komponenten aus dem Ergebnisvektor x
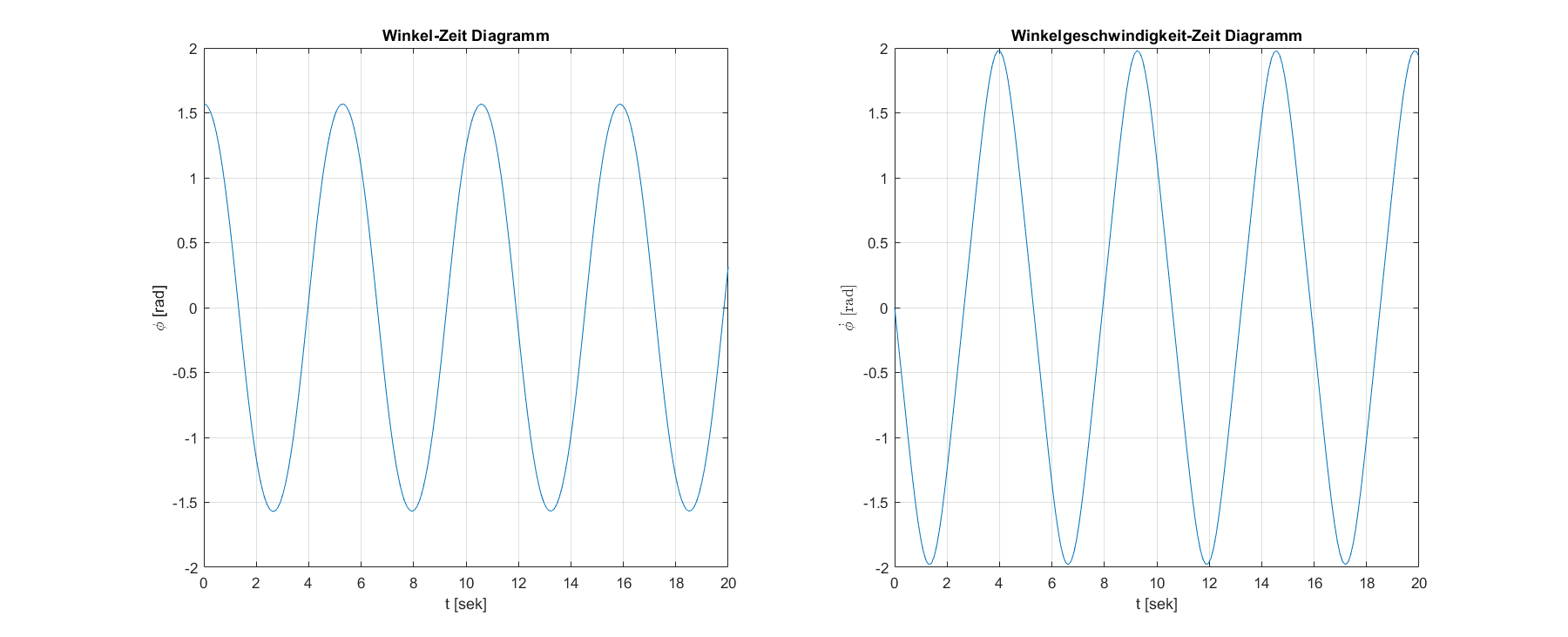
Abbildung 2: Mit Hilfe des plot-Befehls können wir nun unsere Diagramme zeichnen lassen, diese sollten ungefähr so aussehen.
Tipp: Mit subplot können mehrere Plots nebeneinander dargestellt werden!
plot(t, phi_t)
grid on
title('Winkel-Zeit-Diagramm')
Neben statischen Diagrammen ermöglicht Matlab die Animation von Bewegungen. Dies gelingt, indem für jeden Zeitschritt der schon bekannte Plot-Befehl ausgeführt wird. Mit dem Befehl hold kann erzwungen werden das Darstellungsfenster geöffnet zu halten und den neuen Datenpunkt hinzuzufügen. So sollte es Ihnen gelingen eine ähnliche Animation des Winkel-Zeit-Diagrams zu generieren, wie unten dargstellt ist. Leider können Animationen nicht interaktiv auf dieser Seite ausgeführt werden, kopieren Sie den Code in Matlab und füllen Sie die Lücken!
Nutzen Sie die bereitgestellte Code-Struktur, um auch die Bewegung des Pendels zu simulieren.
cartesianx = %zunächst muss der Vektor mit den Winkeln zu allen Zeitpunkten kartesisch ausgedrückt werden
cartesiany =
frame = 1; %Setze den Framezähler initial auf 1
for i = 1 : t_steps %Für jeden Zeitschritt soll ein Plot erstellt werden
%Darstellung des animierten Winkel-Zeit-Diagrams
plot()
%Darstellung Pendel (Die obigen plots sollten nicht überschrieben werden, wie können wir das lösen?)
plotarrayx = [0 cartesianx(iterations)]; %Das ist der x-Anteil des Seil-Vektors (oben berechnet)
plotarrayy = [0 cartesiany(iterations)]; %Das ist der y-Anteil des Seil-Vektors (oben berechnet)
%Jetzt wird einmal die Masse des Pendel als roter Kreis und das Seil als Linie geplotet
plot(cartesianx(iterations),cartesiany(iterations),'ro',plotarrayx,plotarrayy,'k-')
title(['Animation in kartesischen Koordinaten'],'fontsize',12)
xlabel('x [m]','fontsize',12)
ylabel('y [m]','fontsize',12)
axis([-l l -l 0]) %Als Ränder unseres Diagrams können wird jeweils die Länge des Seils setzen
pbaspect([2 1 1]) %Hier wird die Aspect-Ratio des Diagrams so angepasst, sodass 1m in x-Richtung so lang ist, wie 1m in y-Richtung
iter = iter+1;
end
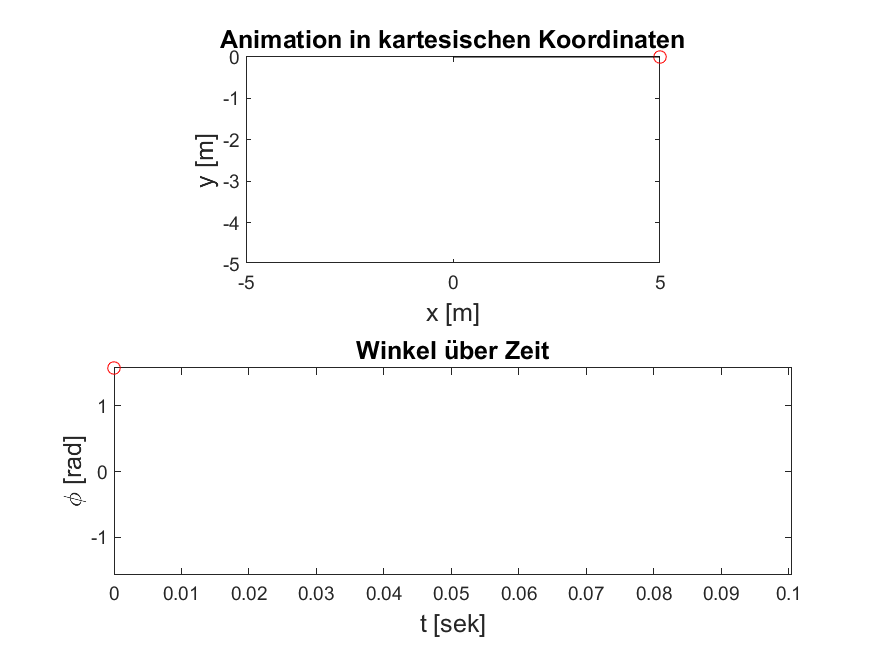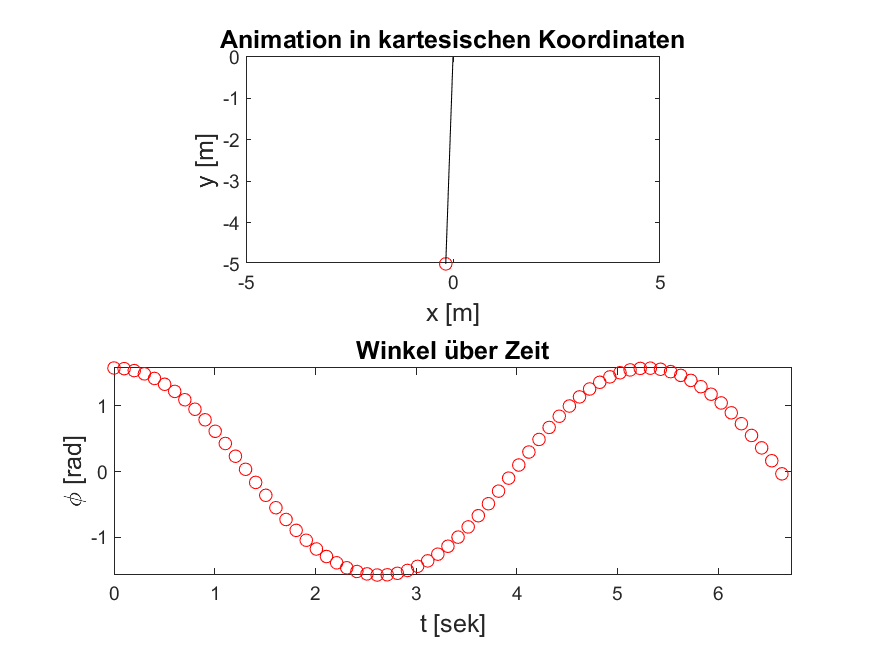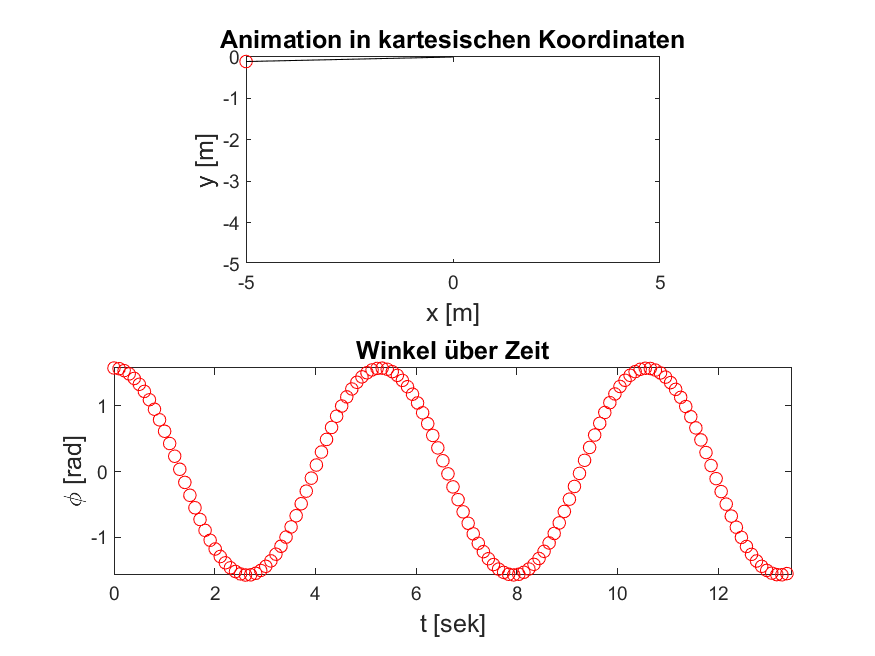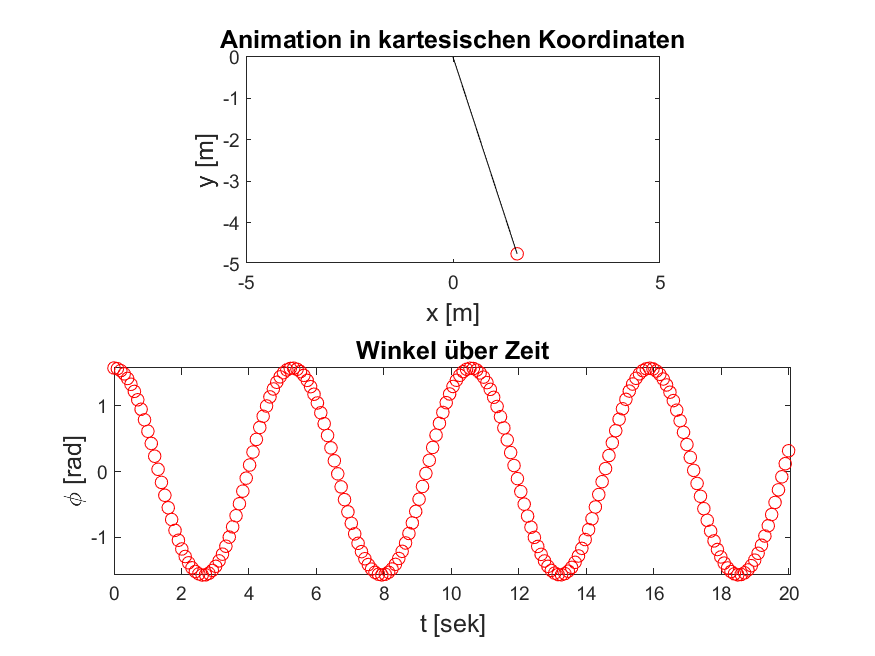
Abbildung 3: Ihr Ergebnis sollte den hier gezeigten Animationen ähnlich sein. Je nachdem welche Parameter Sie insbesondere für die Zeitschrittweite und Schrittanzahl wählen, wird es sich unterscheiden.
Experimentieren Sie mit den Parametern herum: Verhält sich das Pendel immer Ihrer Erwartung entsprechend?
Welche Parameter müssen Sie wählen, um bei den oben genannten Anfangsbedingungen eine Periodendauer von 10 Sekunden zu erreichen?
Aufgabe 2: Dämpfung#
Vergleicht man die bisherigen Ergebnisse mit realen Pendeln wird schnell ersichtlich, dass wir hier etwas realistischer modellieren könnten. In Aufgabe 1 wurde die zu lösende Differentialgleichung mit Hilfe des Energieerhaltungssatzes hergeleitet. Dabei sind wir von einem abgeschlossenen System ausgegangen, d.h. weder Masse noch eine andere Energieform kann über Systemgrenzen mit der Umwelt ausgetauscht werden. Dies entspricht natürlich nicht der Realität, insbesondere die Luftreibung entzieht unserem System kinetische Energie und wandelt diese in Wärme um. Die Geschwindigkeit des Pendels wird reduziert. Um diesen Effekt in unserem Modell zu berücksichtigen, müssen wir unserer Differentialgleichung einen Dämpfungsterm hinzufügen.
Auch hier hilft die Energieerhaltung bei der Herleitung der Differentialgleichung. Die dämpfende Kraft soll mit einer Dämpfungskonstanten modelliert werden und ist abhängig von der Winkelgeschwindigkeit!
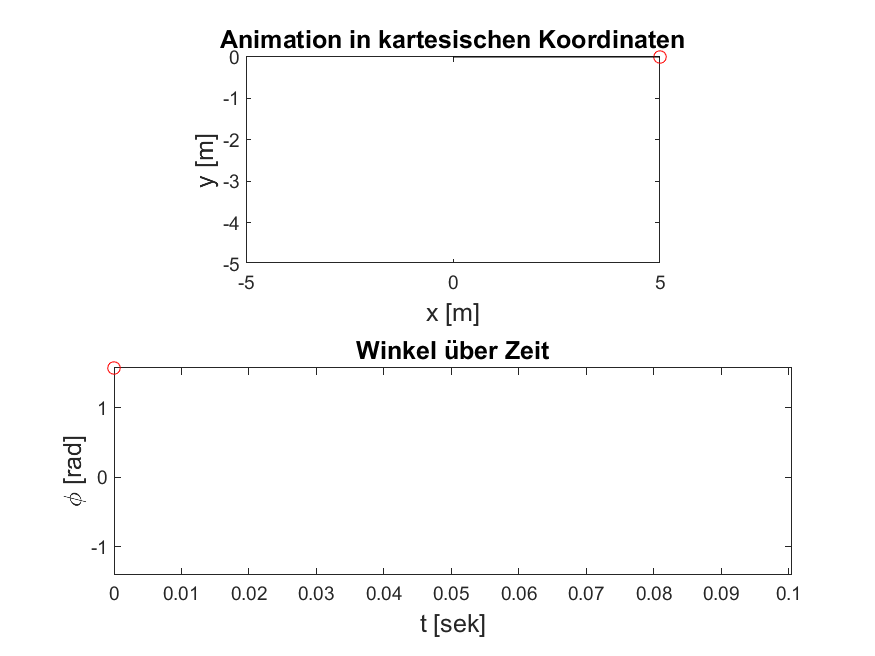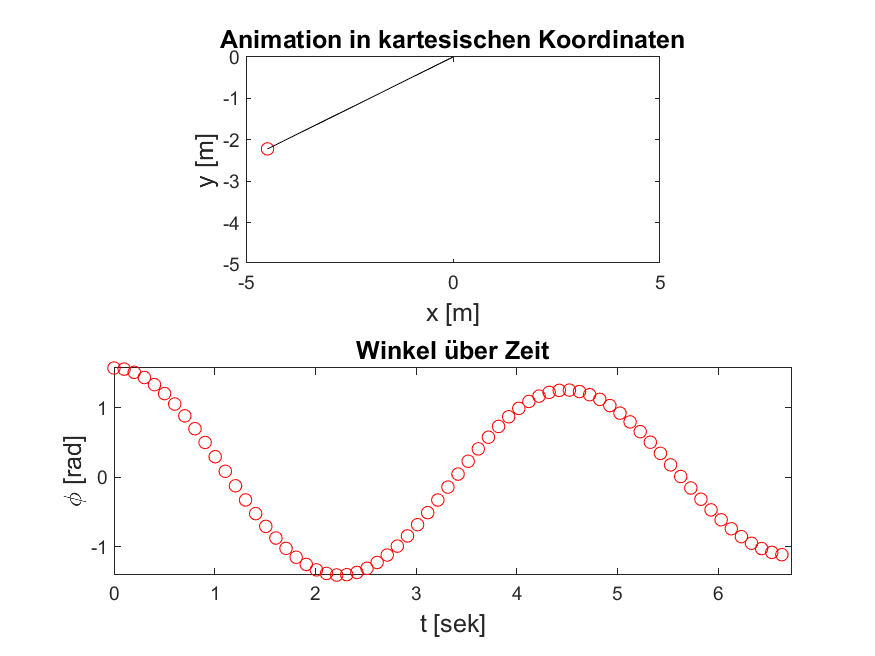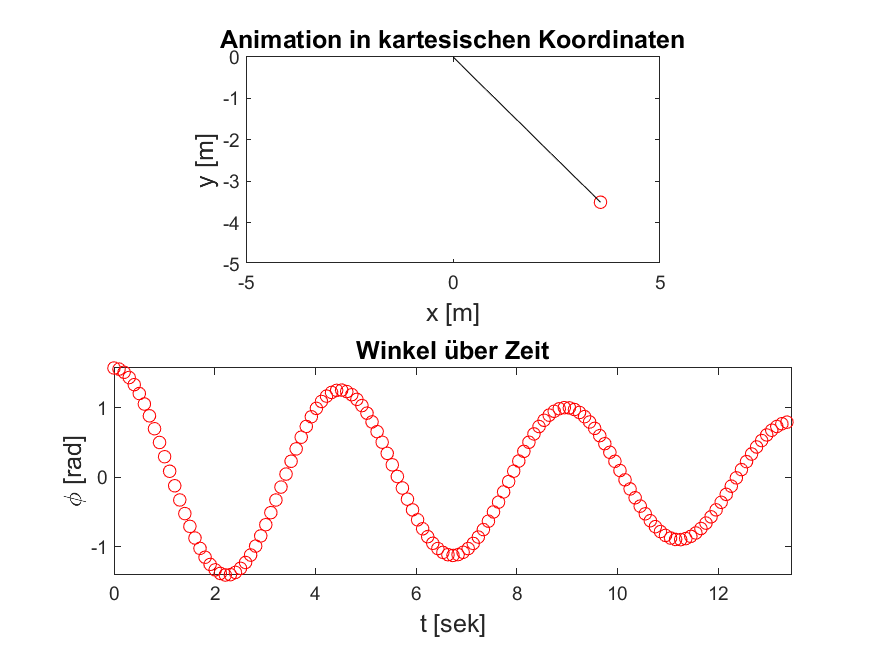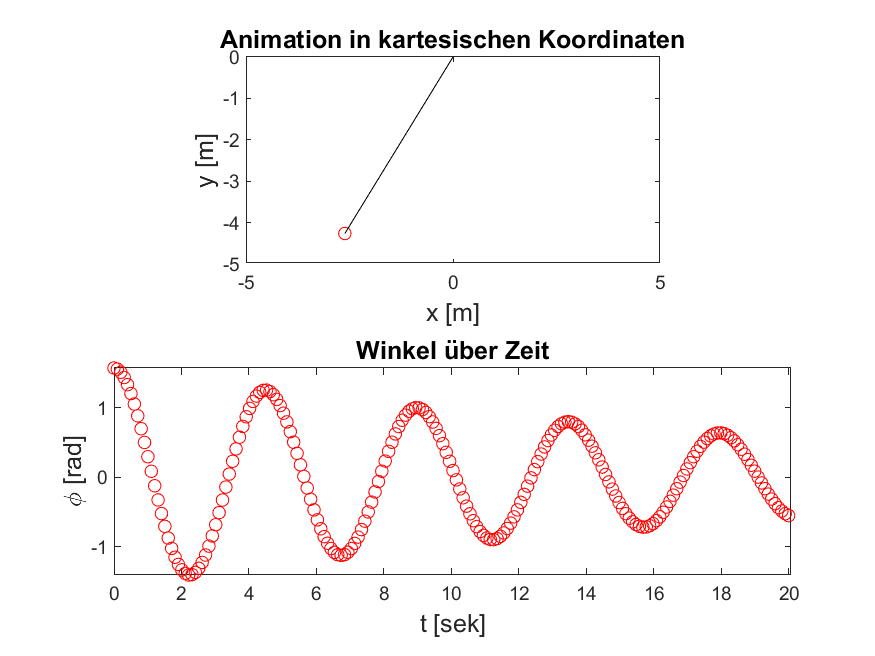
Abbildung 4: Wenn Sie Ihren Code aus Aufgabe 1 erweitern, sollten Sie in Ihrer Animation den dämpfenden Charakter der neuen Differentialgleichung erkennen können. Testen Sie dazu mögliche Dämpfungskonstanten aus.
Mehr zu Erhaltungssystemen und ihrer Klassifzierung gibt es hier.
Aufgabe 3: Angeregte Schwingung#
Abschließend soll die Simulation um die Anregung einer beliebigen externen Kraft erweitert werden. Wie muss sich dazu die Differentialgleichung ändern? Simulieren Sie eine periodische Anregung und testen Sie verschiedene Anregungsfrequenzen. Was passiert, wenn Sie mit der Eigenfrequenz des Systems anregen? Tipp: \(\omega_0 = \sqrt{\frac{k}{m}}\)
Tatsächlich hätten wir die bisherigen Aufgaben auch analytisch lösen können und wollten nur Arbeit sparen. Diese neue Differentialgleichung können wir aber tatsächlich gar nicht mehr selbst lösen, spätestens jetzt sind wir also auf einen Löser, wie z.B. ode45, angewiesen!
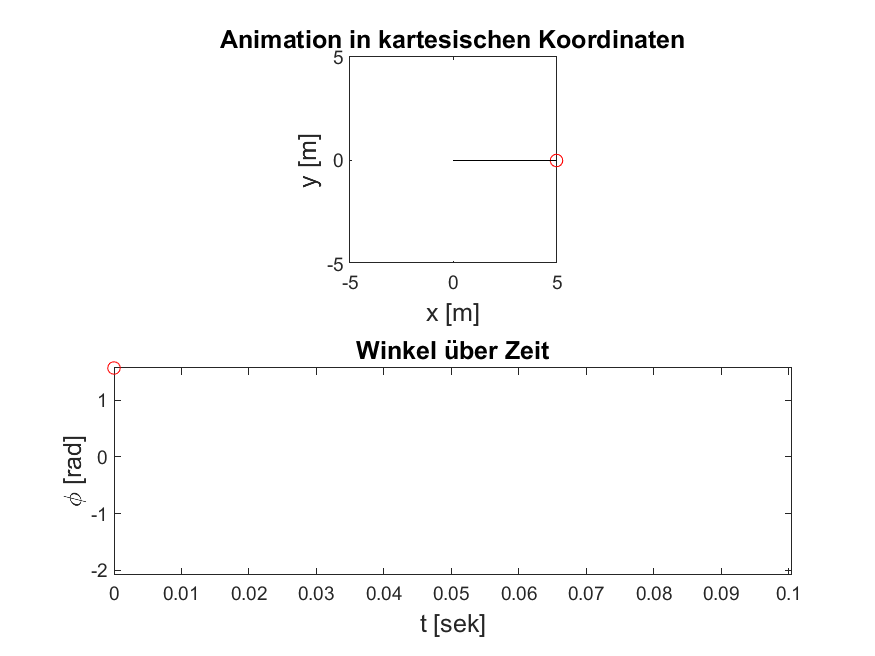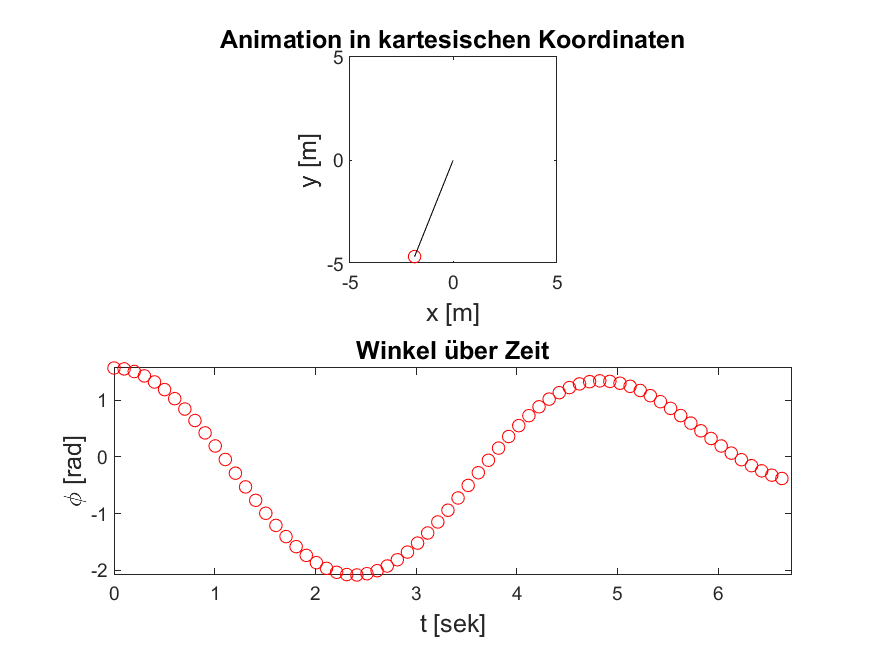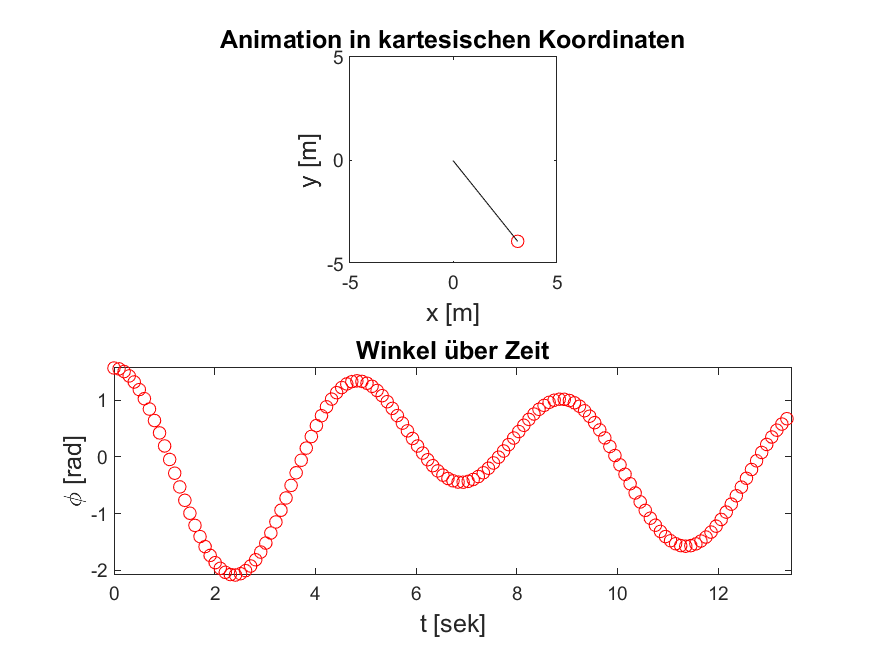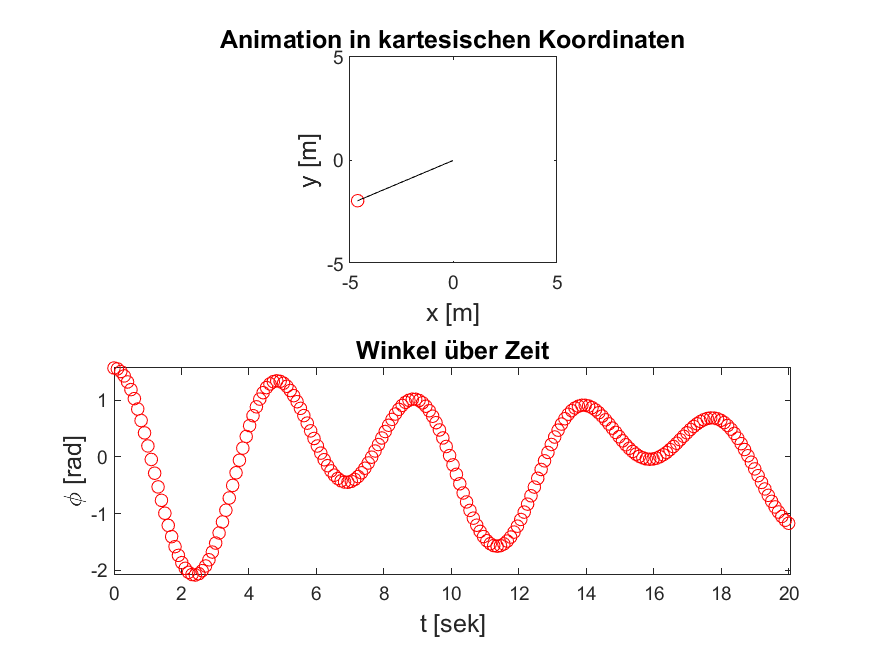
Abbildung 5: Je nach Anregungsfrequenz und -amplitude, werden Ihre Ergebnisse unterschiedlich aussehen. Bei einer Anregungsfrequenz \(\omega = \frac{\omega_0}{2}\) sollten Sie folgende Simulation erzeugen können.
Tipp: Sie können axis() so verändern, dass positive y-Werte dargestellt werden können.
Wählen Sie eine Dämpfungskonstante \(d = 0.3~\frac{kg}{s}\) und simulieren Sie eine periodische Kraftanregung mit einer Amplitude \(A = 1\) und einer Anregungsfrequenz \(\omega = 0.8\), alle anderen Werte wählen Sie wie in Aufgabe 1. Nach welcher Zeit \(t\) wird der eingeschwungene Zustand erreicht? Wie groß ist die Amplitude dieser harmonischen Schwingung? Berechnen Sie die analytischen Lösung und vergleichen Ihre Ergebnisse.

