Ctrl+K

7. Gewöhnliche Differentialgleichungen

7. Gewöhnliche Differentialgleichungen#

Diese Übung beschäftigt sich mit ODEs (Ordinary Differential Equations).

In Aufgabe 1 wird das sog. “Inverse Tangentenproblem von Leibniz” gelöst.

Aufgabe 2 beschäftigt sich mit der Simulation eines einfachen RCL-Schwingkreis mit anliegender Wechselspannung.

1. Inverses Tangentenproblem („Taschenuhrproblem“)#

Lösen Sie das inverse Tangentenproblem von Leibniz:

Auf welcher Bahn y(x) bewegt sich die Taschenuhr, wenn sie entlang ihrer Kette der Länge a gezogen wird?

\[y'(x) = \frac{y(x)}{\sqrt{a^2-y^2(x)}}\]
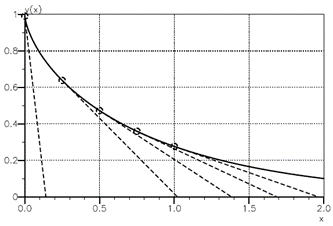
Pocketwatch movement

Hinweis

Legen Sie für die DGL eine eigene function an und lösen Sie diese mit der Matlab-Routine ode45.

function main
    xspan = %...?
    y0 = %...?
    [x,y] = ode45(@dgl,xspan,y0);
    plot(x,y)
end

function dy = dgl(x,y)
    dy = %...?
end

2. RCL-Schwingkreis#

Simulieren Sie den Strom in einem RCL-Schwingkreis mit anliegender Wechselspannung.

RCL Circuit
\[\frac{d^2}{dt^2}i(t) = -\frac{1}{LC}i(t)-\frac{R}{L}\frac{d}{dt}i(t)-\frac{1}{L}\frac{d}{dt}u(t)\]

Prüfen Sie das Verhalten des Schwingkreises mit den beiden Parametersets:

Schwingkreis Parameter 1:
\(R = 0, 1, 10, 100, 1000\)
\(C = 0.01\)
\(L = 0.01\)

Schwingkreis Parameter 2:
\(R = 10\)
\(C = 0.01\)
\(L = 1, 0.1, 0.01, 0.001, 0.0001\)

Für die anliegende Wechselspannung gilt:

\[U(t) = 5\cdot\sin(50\cdot 2\pi\cdot t) [V]\]

Hinweis

Transformieren Sie die DGL zweiter Ordnung auf zwei DGLs erster Ordnung und legen Sie für das resultierende DGL-System eine separate function an, welche Sie mit ode45 lösen.

function main
    tspan = [0, 0.5];
    y0 = %...?
    [t,y] = ode45(@dgl,tspan,y0);
    plot(t,y(:,1))
end

function dy = dgl(t,y)
    dy(1,1) = %...?
    dy(2,1) = %...?
end

Lösung#

- Hinweis: Dieses Video ist von YouTube aus eingebunden und nicht Teil des frei lizenzierten Materials! -

Contents