Voraussetzungen
Programmier-Grundlagen
Kinematik-Grundlagen
Lerninhalte
vertiefte Übung der Modellbildung
Sensibilisierung für die mathematische Robustheit (Abweichung des Ergebnisses bei Abweichung der Eingabewerte) eines Modells
Der perfekte Wurf#
Man könnte annehmen, dass das (erfolgreiche) Werfen eines Freiwurfs für alle hochbezahlten Basketballstars eine reine Formalität ist. Erstaunlicherweise ist dem nicht so! Während der deutsche NBA Star Dirk Nowitzki in der Saison 2008/09 laut NBA Media Ventures (2009) immerhin eine Trefferquote von 89% hatte, gibt es andere NBA Superstars, die in dieser Hinsicht weniger erfolgreich sind. Ein prominentes Beispiel ist Shaquille O’Neal, der am Ende der Saison 2008/09 gerade einmal eine Trefferquote von 59% hatte, in seiner gesamten Karriere sogar nur eine Quote von 52.4%. Er ist kein Einzelfall: Fast ein Drittel der NBA-Spieler haben beim Freiwurf eine Trefferquote von weniger als 75%. Für uns stellt sich die Frage: Woher kommen diese Unterschiede und ist es eventuell möglich ein Modell zu erstellen, das den ’perfekten Wurf’ wiedergibt?
Modellbeschreibung#
In Abbildung 2 sind die Messungen eines aufgezeichneten Wurfes dargestellt. Der Ball geht ins Netz, wobei er knapp die Hände von Spieler B streift. Die Größe des Balles wird hier vernachlässigt und das Problem wird nur in zwei Dimensionen betrachtet. Der Ball vollführt eine geradlinige Bewegung in horizontaler Richtung und eine gleichförmig beschleunigte Bewegung in vertikaler Richtung. Das Koordinatensystem kann frei gewählt werden, hier wird der Ursprung an die Position des werfenden Spielers auf Bodenhöhe gelegt. Dabei soll die \(x\)-Achse in Richtung des Baseketballkorbes und die \(y\)-Achse nach oben zeigen.
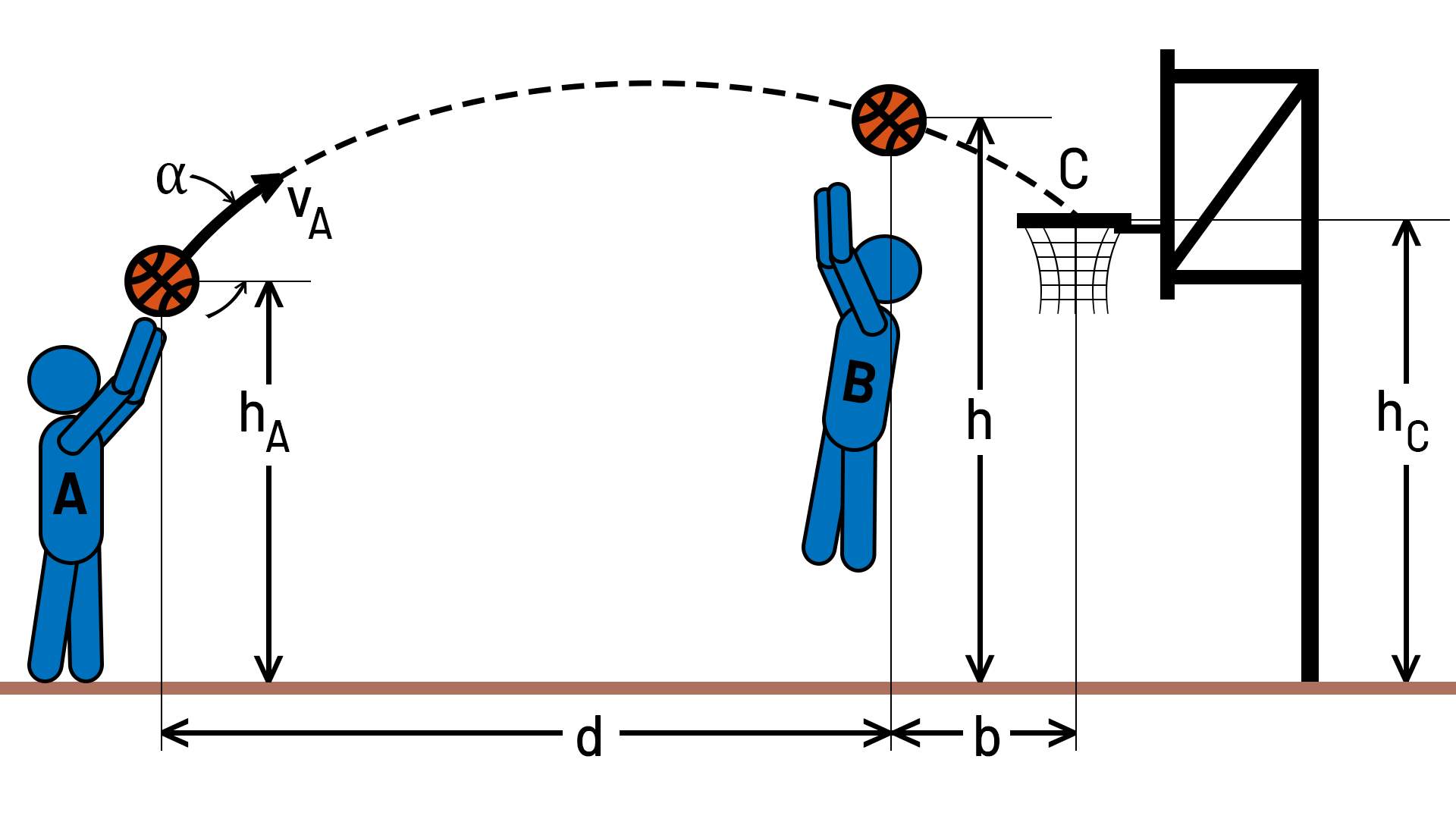
Aufgabe 1: Aufstellen der Bewegungsgleichung#
Zunächst soll mit Bleistift und Papier die Grundlage geschaffen werden, um in den folgenden Aufgaben mit Hilfe von Matlab den Wurf eines Basketballes zu simulieren. Die Bewegungsgleichungen in \(x\)- und \(y\)-Richtung können leicht für die gegebene Bewegung hergeleitet werden.
In \(x\)-Richtung wird der Ball nicht beschleunigt, er besitzt aber eine Anfangsgeschwindigkeit in \(x\)-Richtung \(v_x\). Wegen der Wahl des Ursprungs gilt außerdem \(x(t=0)=0\).
a) Stellen Sie die Bewegungsgleichungen in x-Richtung auf.
\(x''(t) =\)
\(x'(t) =\)
\(x(t) =\)
In vertikaler Richtung wird der Ball mit der Erdbeschleunigung \(g = 9.81 \;\mathrm{m/s^2}\) beschleunigt und besitzt eine Anfangsgeschwindigkeit in \(y\)-Richtung \(v_y\) und eine Abwurfhöhe von \(h_A\).
b) Stellen Sie die Bewegungsgleichungen in \(y\)-Richtung auf.
\(y''(t) =\)
\(y'(t) =\)
\(y(t) =\)
Mittels einfacher Trigonometrie können \(x(t)\) und \(y(t)\) als Funktionen des Abwurfwinkels \(\alpha\) und des Betrags \(v_a\) ausgedrückt werden. Führen Sie sich diesen Zusammenhang, wenn nötig, mit Hilfe einer einfachen Skizze vor Augen.
c) Stellen Sie \(x(t)\) und \(y(t)\) als Funktionen des Abwurfwinkels dar.
\(x(t) =\)
\(y(t) =\)
Modellierung#
Mit Hilfe der zuvor aufgestellen Bewegungsgleichungen sollen im Folgenden verschiedene Freiwurf-Szenarien simuliert werden.
Aufgabe 2: Freiwurf eines punktförmigen Balles#
Schreiben Sie auf Basis der zuvor aufgestellten Bewegungsgleichungen ein Programm, in welchem Sie die Bahnkurve des Balls beim Freiwurf für beliebige Abwurfwinkel \(\alpha\) berechnen können. Am Ende dieser Seite steht dazu bereits ein Code-Gerüst. Dieses können Sie interaktiv auf dieser Seite nach und nach füllen und ausführen, oder in Matlab kopieren. Die Aufgaben sind so strukturiert, dass Sie Ihr Skript zur Lösung jeder weiteren Aufgabe erweitern können.
Gehen Sie von einem punktförmigen Ball aus; einen gültigen Wurf erhalten Sie dann, wenn der Ball mittig im Korb landet. Binden Sie Korb und Brett in die Visualisierung ein. Verwenden Sie folgende Maße für die Beschreibung des Problems (Maße für alle Aufgabenteile):
Parameter |
Wert \([\mathrm{m}]\) |
|---|---|
Abwurfhöhe |
\(2.31\) |
Korbhöhe |
\(3.05\) |
Korbradius |
\(0.225\) |
Wurfdistanz |
\(4.115\) |
Höhe Unterkante Brett |
\(2.9\) |
Vertikale Länge des Bretts |
\(1.05\) |
Abstand Brett-Korb |
\(0.15\) |
a) Abwurfwinkel#
Überlegen Sie sich, welche Abwurfwinkel realistisch sind und legen Sie auf dieser Basis ein Intervall fest, für das Sie Würfe simulieren wollen. Plotten Sie innerhalb dieses Intervalls alle Bahnkurven im Abstand von 0.1 Grad.
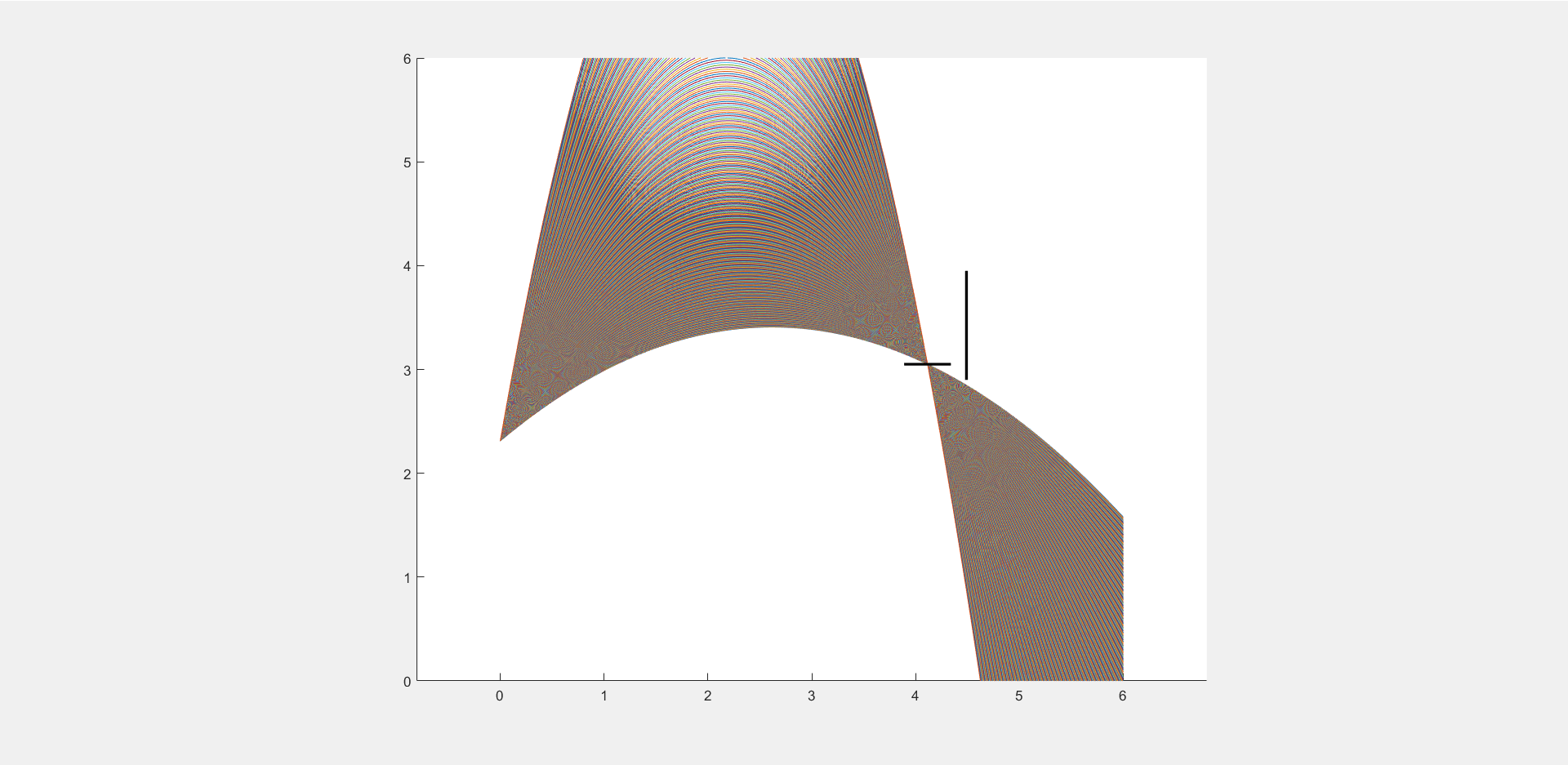
b) Anpassen der Korbgröße#
Der Korb ist in der Realität größer als der Ball, so dass dieser für einen Treffer nicht exakt mittig durch den Korb fallen muss. Erweitern Sie ihr Programm so, dass der Ball an jedem Punkt durch den Korb fallen kann. Gehen Sie dann von \(\theta = 60^\circ\) aus und variieren Sie die Anfangsgeschwindigkeit. Zwischen welchen Werten darf die Anfangsgeschwindigkeit nun für einen Treffer schwanken? Visualisieren Sie die Bahnkurve für die minimale, maximale und optimale (Ball landet mittig im Korb) Anfangsgeschwindigkeit.
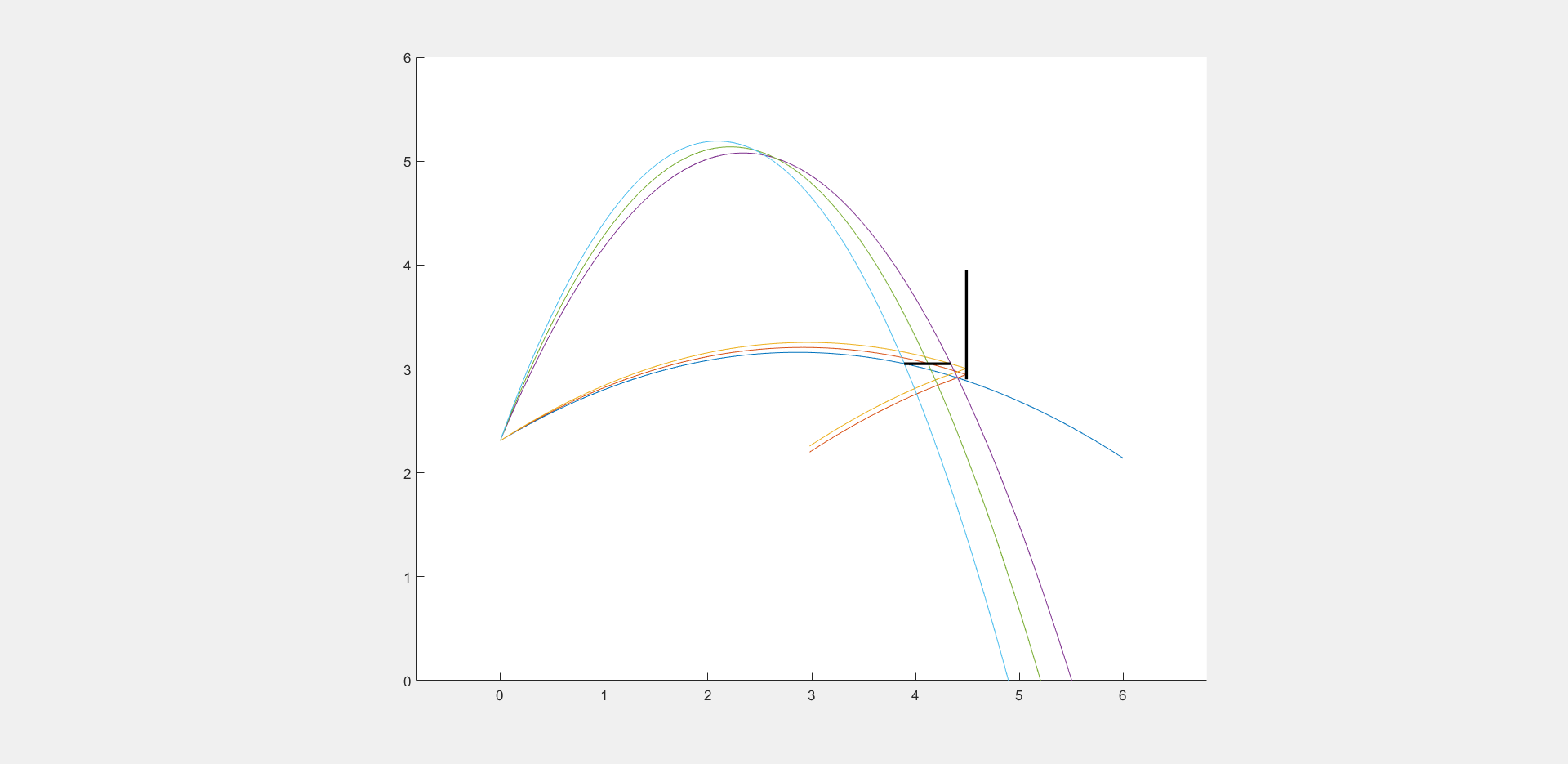
c) Niemand ist perfekt!#
Niemand ist in der Lage den optimalen Abwurfwinkel bei jedem Wurf zu treffen, dieser schwankt in der Realität. Gehen Sie nun von \(\theta = 60^\circ\) plus einem zufälligem Verwackler von \(\pm 5^\circ\) (im Mittel, max. \(\pm 12^\circ\)) aus. Wie viele Treffer werden nach 1000 Würfen in etwa erzielt? (Mittelwert und Standardabweichung!)
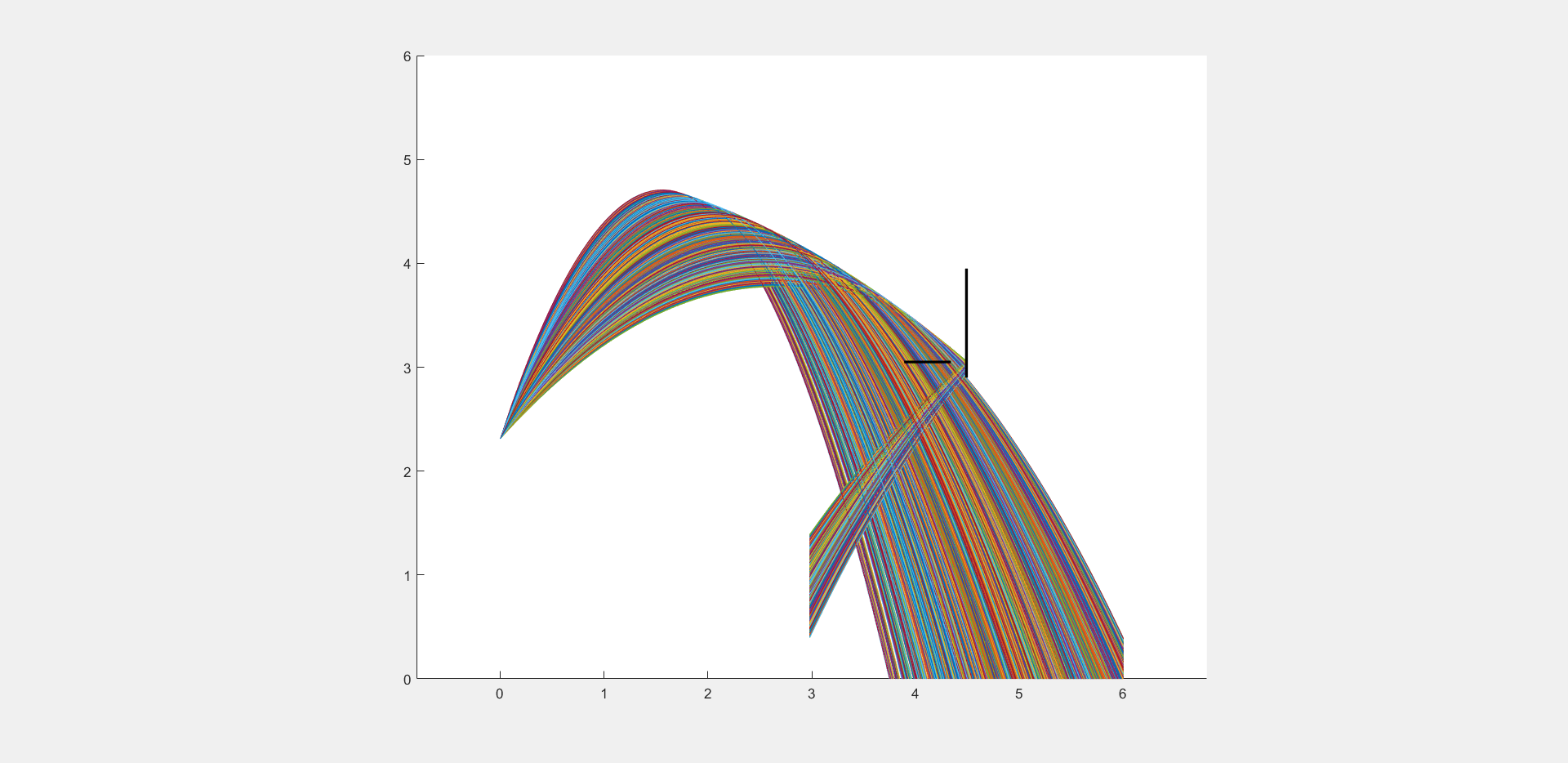
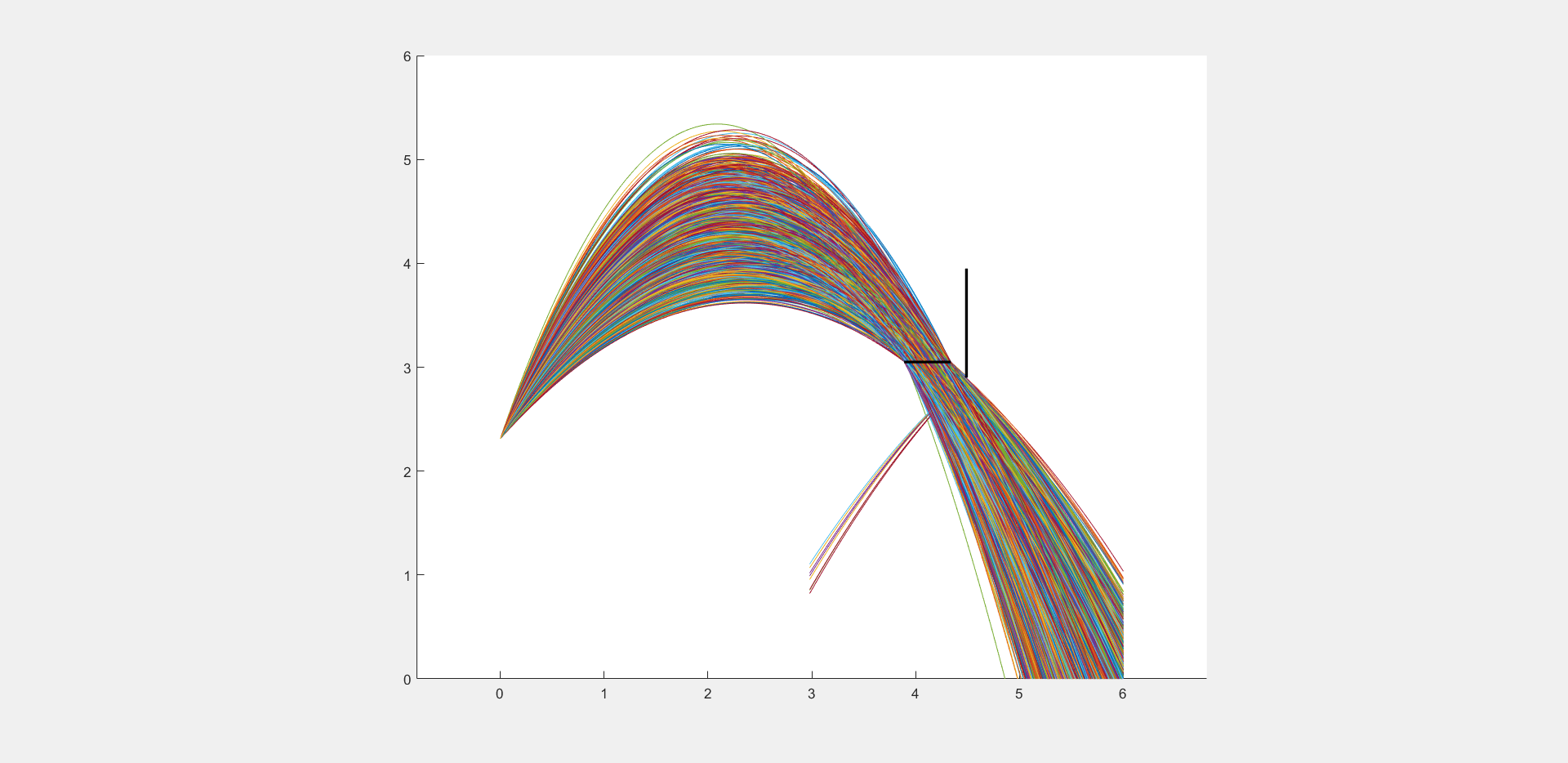
d) Abweichungen in der Abwurfgeschwindigkeit#
Erweitern Sie Ihr Programm so, dass zusätzlich ein Fehler in der Abwurfgeschwindigkeit von \(\pm 0.5\frac{\mathrm{m}}{\mathrm{s}}\) (im Mittel, max. \(\pm 1\frac{\mathrm{m}}{\mathrm{s}}\)) berücksichtigt wird. Wie viele Treffer werden mit dieser zusätzlichen Eigenschaft nach 1000 Würfen in etwa erzielt (\(\theta = 60^\circ\))?
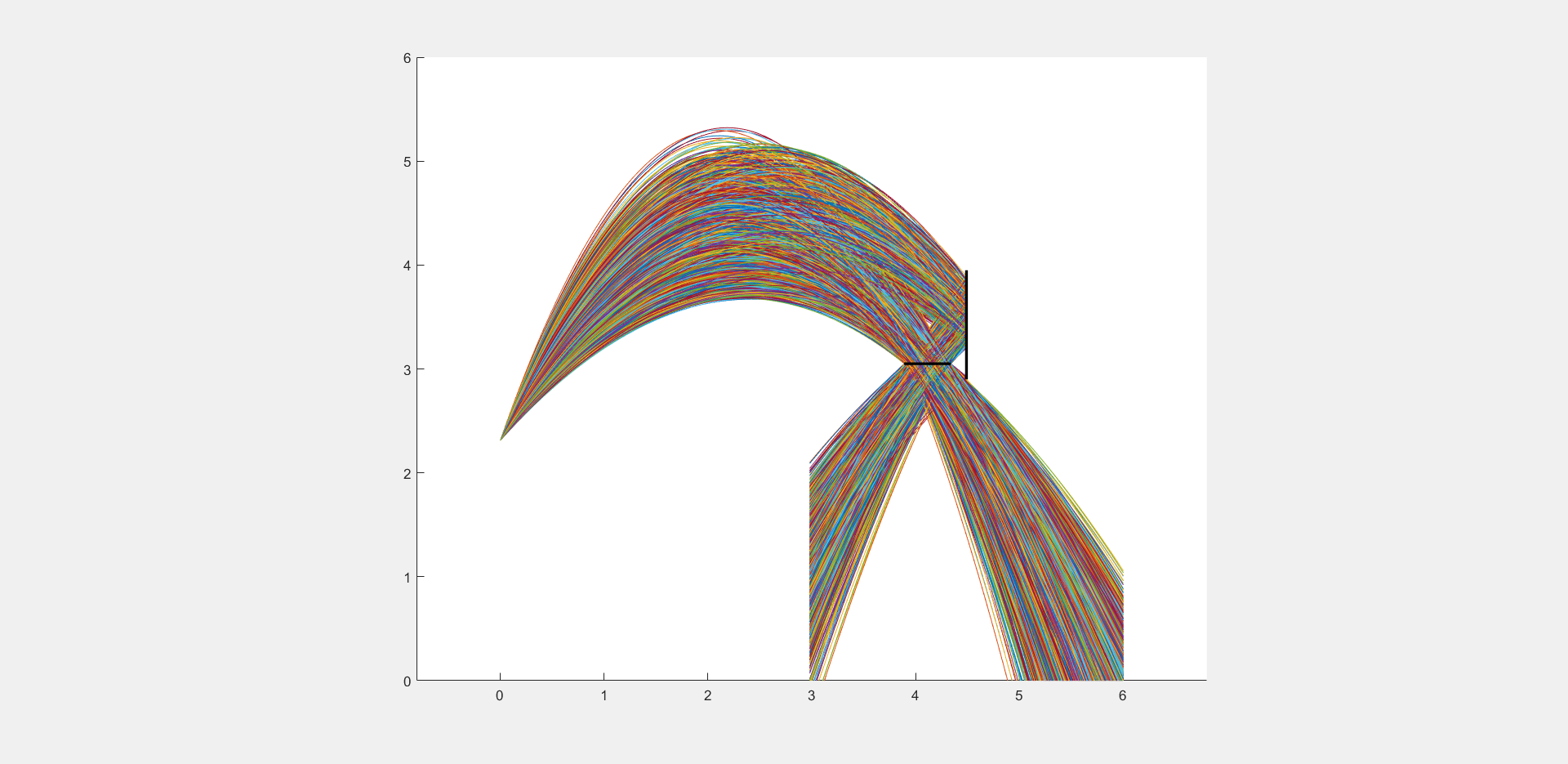
e) Bank Shots erlaubt!#
Erweitern Sie Ihr Programm so, dass der Ball beim Auftreffen am Brett ideal elastisch zurückgestoßen wird. Wie viele Treffer werden nun erzielt (\(\theta = 60^\circ\))?
Hinweis
Beachten Sie den Abstand zwischen Korb und Brett.
f) Ausblick#
Nennen Sie mindestens drei Einflussfaktoren eines realen Basketballwurfes, die bisher nicht in das Modell eingeflossen sind. Beschreiben Sie kurz (3-5 Sätze) wie Sie das Modell um mindestens einen dieser Faktoren möglichst einfach erweitern könnten. Stellen Sie sich vor, Sie sind Coach und möchten Ihr Modell im Training einsetzen. Was kann Ihre Mannchaft aus Ihren Simulationen lernen? Schreiben Sie 3-5 Sätze dazu. Wie können Sie Ihr Modell durch Messungen im Training validieren? keine Programmierung
% Umgebungskonstanten
% Wurfparameter
% Wurfwinkel
%Vorgabe von Winkelintervallen
% Wurfgeschwindigkeit
% Visualisierungsparameter
%%%% HAUPTPROGRAMM
% Berechnung der Sollwinkel für alle Würfe
% Berechnung der Sollgeschwindigkeit für alle Würfe
% Berechnen der optimalen Geschwindigkeiten in m/s,
% falls keine Geschwindigkeit vorgegeben
% Hilfsvariablen
% Schleife über mehrere Wurfserien
for s=1:n_serien
%Vorinitialisierung von Vektoren
% Schleife über Würfe
for i = 1:n_wuerfe
% Addieren von zufälligen Winkelabweichungen
% Addieren von Zufällige Geschwindigkeitsabweichungen
% Berechnung der Ballhöhe am Brett
% Trifft Ball das Brett?
% Berechnung der Weite bei Korbhöhe
% Zählen der direkten Treffer
% Zählen der Treffer über Brettabpraller
% Berechnung der Trajektorien
end
% Änderung der Trajektorien bei Abprallern
% Plot der gewünschten Flugkurven
end
% Koordinatensystem
% Plot des Korbes und des Brettes
% Ausgabe der Trefferstatistik für diese Wurfserie
end
% Statistik über alle Wurfserien

