Ctrl+K

Lineare Approximation

Voraussetzungen

  • mathematische Grundlagen der linearen Approximation

Lerninhalte

  • Realisierung einer Routine zur linearen Approximation

Lineare Approximation#

Aufgabe 1#

Erzeugen Sie sich auf Basis folgender Geradengleichung \( y = 2.2 x - 3.1 \) Werte im Intervall \(x \in [0,10]\). Modifizieren Sie die entsprechenden y-Werte so, dass diese normalverteilt von der exakten Geradengleichung abweichen (Abbildung). Gehen Sie dabei zunächst von \(n=100\) Messwerten aus.

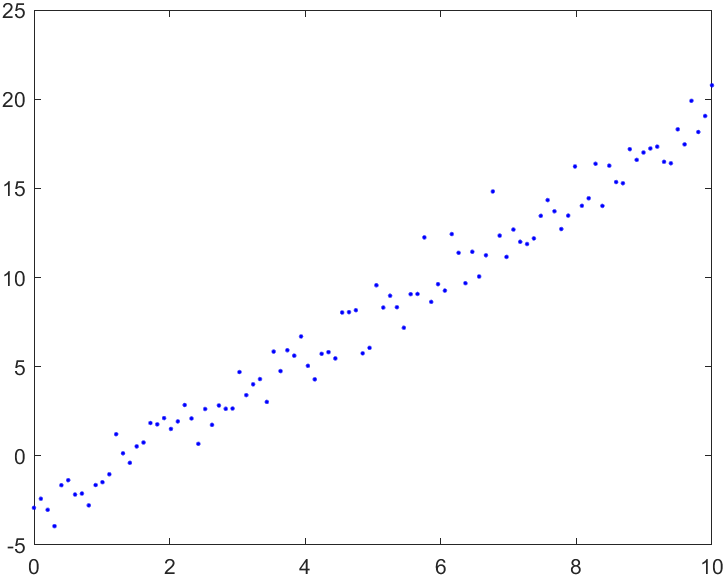
../_images/approx.png
Abbildung 1: Normalverteilt um die Gerade y(x) gestreute Werte als Punktewolke. 

n=100
x=linspace(0,10,n)

y=f(x)              %Erzeugen der y-Werte mittels zu erstellender Funktion f(x)
y=y+randn(size(y))  %Erstellen des Störsignals

Aufgabe 2#

Sie haben eben (in Aufgabe 1) die Messwerte simuliert. Sie wollen diese Punkte nun mit Hilfe eines Polynoms approximieren. Schreiben Sie dazu ein Programm, welches eine Regressionsgerade durch diese Punkte legt.
Verwenden Sie dabei nicht die polyfit-Funktion! Berechnen Sie stattdessen die Koeffizienten der Regressionsgeraden.

Kurzer Rückblick

Die Gleichungen

\[ \sum_{j=0}^m a_j \sum_{i=0}^n x_i^{j+k} = \sum_{i=0}^n y_i \, x_i^k \, , \; k=0,...,m \]

nennen wir die Normalengleichungen.
Sie definieren ein lineares Gleichungssystem für die Koeffizienten \(a_k\).

Für den Polynomgrad \(m=1\) ergibt sich beispielsweise das System:

\[\begin{split} \begin{pmatrix} n+1 & \sum x_i \\ \sum x_i & \sum x_i^2 \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \end{pmatrix} = \begin{pmatrix} \sum y_i \\ \sum y_i x_i \end{pmatrix} \end{split}\]

Dabei entspricht \(n+1=\) der Anzahl der Messwerte.

% SPACE FOR THE SOLUTION

Aufgabe 3#

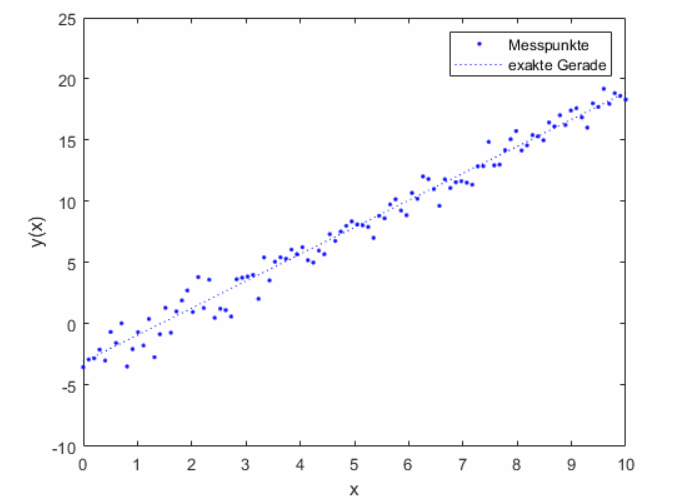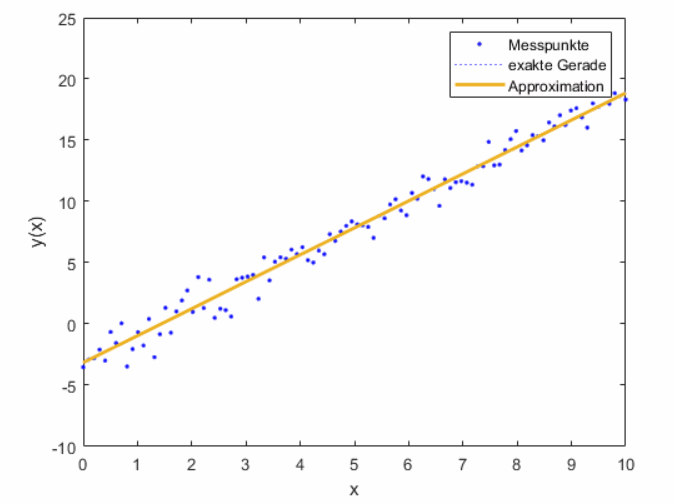
Stellen Sie nun die Messpunkte, die Regressionsgerade und die exakte Geradengleichung in einem Plot graphisch dar (siehe Abbildung 2).

Testen Sie außerdem, wie sich die Regressionsgerade (also die Approximation der Messpunkte) bei kleinem bzw. großem \(n\) verhält. Überlegen Sie sich dabei selbst, was “klein” bzw. “groß” bedeutet und begründen Sie ihre Wahl. Gibt es Werte für \(n\) für die diese Art der Approximation ungeeignet ist?

../_images/approx.gif
Abbildung 2: Die Gerade y(x) (blau gestrichelt). Darum normalverteilt gestreute Werte als Punktewolke (blau) und die aus den Punkten linear approximierte Gerade (orange). 

% SPACE FOR THE SOLUTION
Contents