Ctrl+K

Numerische Integration (mit Schrittweitensteuerung)

Voraussetzungen

  • Programmier-Grundlagen

  • einfache Annäherungsformeln für Integrale

Lerninhalte

  • Grundlagen und Realisierung numerischer Integration

  • Grundlagen und Realisierung numerischer Schrittweitensteuerung

  • Validierung von Programmroutinen mittels Unit Tests

Numerische Integration (mit Schrittweitensteuerung)#

Aufgabe 1: Vorarbeit mit Stift und Papier#

Entwickeln Sie mit Stift und Papier (und am besten auch einer Skizze) die Trapezregel zur numerischen Approximation von Integralen beliebiger Funktionen auf beliebigen Intervallen.

Aufgabe 2: Numerische Integration#

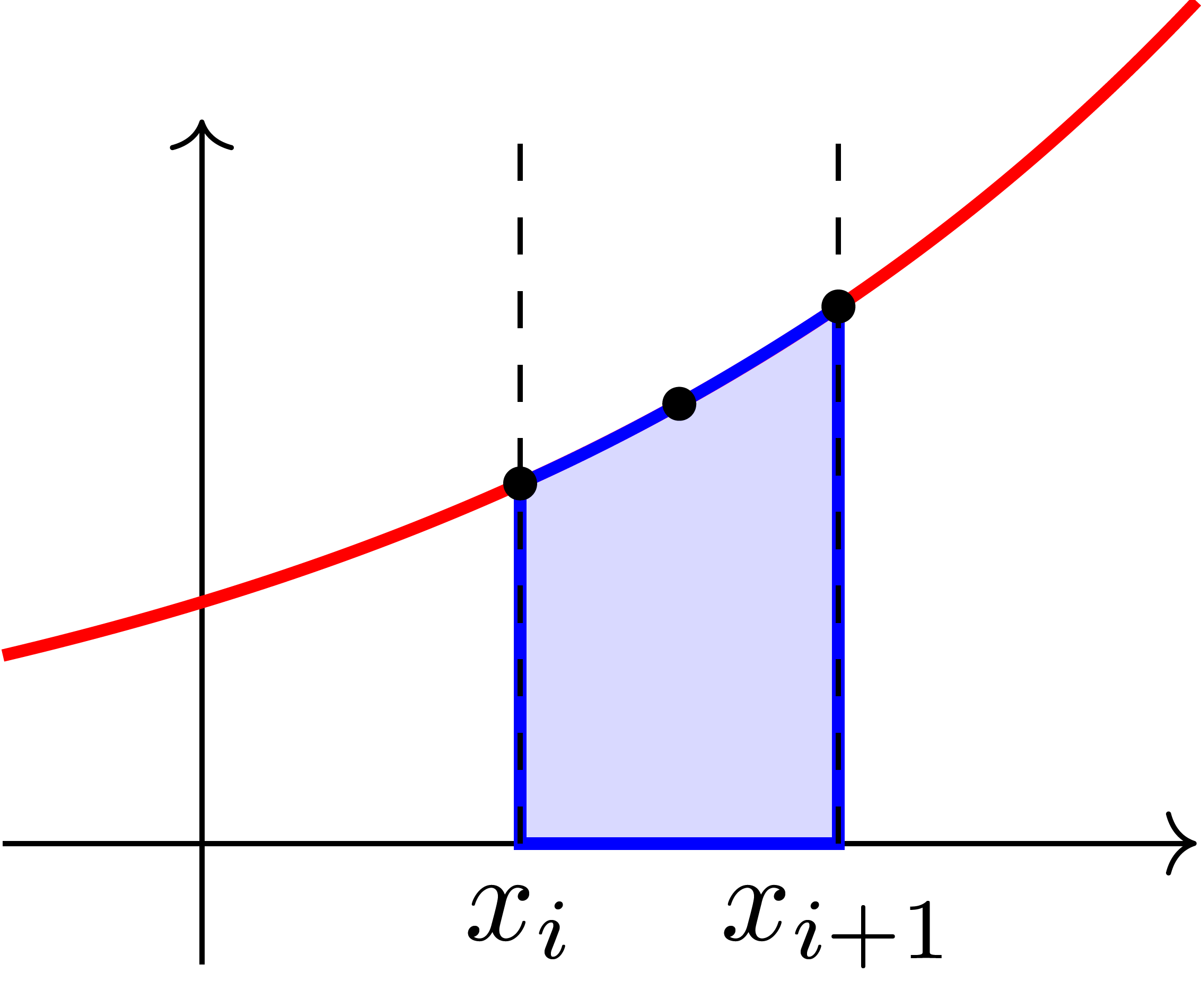
Die Simpson-Regel erweitert dieses Konzept. Statt einer Geraden wird hier zur Approximation eine Parabel durch die Randpunkte und den Mittelpunkt des Intervals gelegt und der Flächeninhalt darunter bestimmt. So kann die Fehlerordnung der Approximation erhöht werden. Die Integrationsformel lautet dann

\[\int_{x_i}^{x_{i+1}} f(x) dx = \frac{x_{i+1} - x_i}{6}\left(f(x_i)+4f\left(\frac{x_i+x_{i+1}}{2}\right)+f(x_{i+1})\right).\]
Name of image

Schreiben Sie ein Programm zur numerischen Berechnung von \(\int_{a}^{b} f(x) dx\) mit der zusammengesetzten Simpson- und Trapezregel. Das heißt, beide Regeln werden auf einzelne Teilintervalle angewendet und die Ergebnisse zum Gesamtintegral aufsummiert. Vergleichen Sie die Lösungen für verschiedene Funktionen (beispielsweise \(e^{-x}, \sin(x), x^2, ...\)).

Achtung

Denken Sie daran, dass Eingaben nicht immer mit der Funktionsweise Ihrer Funktion kompatibel sein müssen! Wie geht Ihre Funktion beispielsweise mit der Polstelle um, wenn jemand \(\int_{-1}^{1} \frac{1}{x} dx\) berechnen möchte? Überlegen Sie sich eine Abbruchbedingung für den Fehlerfall!

%%file numInt.m
%function [I, dt]= numInt(f,a,b,tol)
% Compute numeric integral of f on [a, b] to tolerance tol via Simpson's rule. Step width is regulated via comparison to result of Trapezoidal rule.
% Inputs: function, lower boundary, upper boundary, tolerance
% Output: integration result, step size

function [I, dt] = numInt(f,a,b,tol)
% insert your code here
end

Aufgabe 3: Integration mit Schrittweitensteuerung#

Nun soll die Anzahl der verwendeten Teilintervalle so lange verdoppelt werden, bis die Differenz zwischen Simpson- und Trapezregel kleiner als die vom Benutzer vorgegebenen Toleranz tol ist.

Der Vergleich der beiden Ergebnisse ermöglicht es, abzuschätzen, bei welcher Anzahl an Teilintervallen die gewünschte Genauigkeit erreicht wird. Durch eine derartige Schrittweitensteuerung kann zusätzlicher Rechenaufwand durch zu kleine Schrittweiten vermieden werden und trotzdem auf allen Intervallen die geforderte Genauigkeit erreicht werden.

Aufgabe 4: Test der Funktionsweise#

Testen Sie Ihre Funktion mit dem Unit Test. Sie sollten zumindest die ersten fünf der acht Anforderungen erfüllen.

test_numInt()

Den Quellcode des Unit Tests können Sie hier ausklappen. Sehen Sie sich das Kapitel Unit Testing an, um Ihre Erinnerung an Unit Tests aufzufrischen.

Es werden die Ergebnisse von sieben Funktionen anhand der analytischen Lösungen (bzw. der numerisch zu erwartenden Reaktion) getestet. Der Vergleich läuft über die Funktion assertVectorsAlmostEqual().

  1. \(\int_0^1 x dx = 0.5\)

  2. \(\int_{-1}^1 x dx = 0.5\). Hier sollte df = 2 sein.

  3. \(\int_0^1 x^5+x dx = \frac{2}{3}\). Hier sollte df= \(2^{-10}\) sein.

  4. \(\int_{-1}^1 e^x dx = e - \frac{1}{e}\). Hier sollte df= \(2^{-9}\) sein.

  5. \(\int_{-1}^1 (1-cos(-0.33x^2-0.1x +1)) dx\). Hier ist eine Schrittweitensteuerung notwendig. Das Ergebnis wird mit der Matlab-Routine integral() getestet.

  6. Das Integral sollte auch von rechts nach links funktionieren für \(\int_1^0 x dx = 0.5\).

  7. Für \(\int_{-0.5}^{1} \frac{1}{x} dx\) dürfte die Schrittweite schnell zu klein werden. Dafür testet test_numInt, ob numInt.m für dieses Integral eine Fehlermeldung auswirft. Das geschieht mit assertExceptionThrown.

  8. Ebenso sollte \(\int_{-1}^{1} \frac{1}{x} dx = 0\) sein.

Klappen Sie die Box aus, um test_numInt näher anzusehen.

Hide code cell source 
function test_suite=test_numInt
% initialize unit tets
    try
        test_functions=localfunctions();
    catch
    end
    initTestSuite;

%%%%%%%%%%%%%%%%%%%%%%%
%     Basic tests     %
%%%%%%%%%%%%%%%%%%%%%%%

function test_numInt_basic
% test function of basic function
    a = 0;
    b = 1;
    f = @(x) x;
    tol = 10^-6;
    [I, df] = numInt(f,a,b,tol);
    assertVectorsAlmostEqual(I,0.5)
    
function test_numInt_negativeStartOfInterval
% test function of negative start of interval
    a = -1;
    b = 1;
    f = @(x) x;
    tol = 10^-6;
    [I, df] = numInt(f,a,b,tol);
    assertVectorsAlmostEqual([I, df],[0, 2])
    
function test_numInt_moreComplexFunction
% test function of x^5 + x
    a = 0;
    b = 1;
    f = @(x) x^5+x;
    tol = 10^-6;
    [I, df] = numInt(f,a,b,tol);
    assertVectorsAlmostEqual([I, df],[2/3, 2^-10]) 
    
function test_numInt_stepsWidth
% test function of exp(x) to see if step width is correct
    a = -1;
    b = 1;
    f = @(x) exp(x);
    tol = 10^-6;
    [I, df] = numInt(f,a,b,tol);
    % !!! width (2^-9) determined via testing !!! 0.001953125000000
    assertVectorsAlmostEqual([I, df],[exp(1) - 1/exp(1), 2^-9]) 
    
function test_numInt_stepsWidth_2
% test function of 1-cos(-0.33*x.^2-0.1*x +1) where step width control is necessary
    a = 0;
    b = 10;
    f = @(x) 1-cos(-0.33*x.^2-0.1*x +1);
    tol = 10^-6;
    [I, df] = numInt(f,a,b,tol);
    assertVectorsAlmostEqual(I,integral(f, a, b)) 
    
%%%%%%%%%%%%%%%%%%%%%%%
% More advanced tests %
%%%%%%%%%%%%%%%%%%%%%%%

function test_numInt_invertedInterval
% test function of inverted interval (start after end)
    a = 1;
    b = 0;
    f = @(x) x;
    tol = 10^-6;
    [I, df] = numInt(f,a,b,tol);
    assertVectorsAlmostEqual(I,-0.5)
  
function test_numInt_poleInIntervall
% test function of 1/x
    a = -0.5;
    b = 1;
    f = @(x) 1/x;
    tol = 10^-6;
    assertExceptionThrown(@() numInt(f,a,b,tol))
    
function test_numInt_symmetricIntegral
% test function of 1/x
    a = -1;
    b = 1;
    f = @(x) 1/x;
    tol = 10^-6;
    [I, df] = numInt(f,a,b,tol);
    assertVectorsAlmostEqual(I,0)

Aufgabe 5: Vergleich mit der Praxis#

Vergleichen Sie Ihre Ergebnisse auch mit der Matlab-Routine Integral. Überlegen Sie sich dazu wichtige Kenngrößen und Testfunktionen.

Hinweis

Neben der reinen Funktion, die Sie jetzt offensichtlich sehr gut realisiert haben, hat der Code allerdings noch weitere Qualitätskriterien. Ein wichtiges Kriterium ist z. B. der Rechenaufwand bzw. die Zeit, die eine Ausführung benötigt. Dieser kann hier noch optimiert werden, indem die berechneten Werte aus der jeweils vorherigen Iteration weiterverwendet werden, wodurch in jeder Iteration nur ein Drittel so viele Werte berechnet werden wie in der einfachen Implementierung. Aber das soll Ihnen vorläufig erspart bleiben.

Contents