Konvektion und Diffusion

Konvektion und Diffusion#

Abbildung 1: "Aedes Albopictus", James Gathany/CDC, [Public domain] via Wikimedia Commons

Wir wollen simulieren, wie sich ein Insektengift in einer Blutbahn ausbreitet. Zum einen wird sich durch ein Diffusionsprozess das Insektengift mit dem Blut vermischen. Zum anderen wird es mit der Fließgeschwindigkeit des Blutes transportiert (Konvektion). Es ergibt sich ein sogenannter Konvektions-Diffusionsprozess. \(\rho(t,x)\) sei die Konzentration des Insektengiftes entlang der Blutbahn.

Die Kontinuitätsgleichung in einer Dimension lautet

\[ 0 = \frac{\partial \rho}{\partial t} + \frac{\partial}{\partial x} J \]

mit einem Massestrom \(J\). Dieser besteht aus einem Diffusionsterm \(-a \frac{\partial \rho}{\partial x}\) der den Konzentrationsgradienten des Insektengiftes ausgleicht, sowie einem Geschwindigkeitsterm \(c\rho\),

\[ J = -a \frac{\partial \rho}{\partial x} + c(t) \rho, \]

wobei \(c(t)\) die Fließgeschwindigkeit des Blutes zum Zeitpunkt \(t\) bezeichnet. Als Vereinfachung gehen wir von einer zeitlich konstanten Fließgeschwindigkeit \(c(t)=c=\text{const}\) aus. Es sollte nicht allzu schwer sein, das Modell zu einem späteren Zeitpunkt durch eine pulsierende Fließgeschwindigkeit zu erweitern.

Setzen wir den Massestrom in die Kontinuitätsgleichung ein, erhalten wir die Konvektions-Diffusionsgleichung

(1)#\[\frac{\partial \rho}{\partial t} + c \frac{\partial \rho}{\partial x} = a \frac{\partial^2 \rho}{\partial x^2}\]

Aufgabe 1: Vorarbeit mit Papier und Bleistift#

Führen Sie eine Diskretisierung des Problems durch (örtlich und zeitlich), um eine Vorschrift zur numerischen Lösung der Gleichung zu ermitteln. Gehen Sie von zeitlich konstanten Dirichlet-Randbedingungen aus. Verwenden Sie für die örtlichen Ableitungen zentrale Differenzenquotienten und für die zeitliche

das explizite Euler-Verfahren (Untersumme)
das Crank-Nicolson-Verfahren (Trapez-Regel)

Gehen Sie wie folgt vor:

Diskretisieren Sie zunächst im Ort, so dass Sie \(N\) neue Funktionen \(y_i(t) \approx \rho(x_i, t), i=1,...,N\) erhalten. Hierbei bezeichnet \(N\) die Anzahl der Diskretisierungspunkte und \(x_i\) bezeichnet den \(i\)-ten Diskretisierungspunkt Ihres Intervals.
Schreiben Sie die approximierte Lösung \(y_i(t_j)\) der inneren Punkte \(i=2,...,N-1\) in einen Vektor

\[\begin{split} \mathbf{y}^{(j)} = \begin{bmatrix} y_2(t_j) \\ \vdots \\ y_{N-1}(t_j) \end{bmatrix} = \begin{bmatrix} y_2^{(j)} \\ \vdots \\ y_{N-1}^{(j)} \end{bmatrix} \end{split}\]
Bringen Sie die Ortsableitungen der DGL auf die rechte Seite, ersetzen Sie die partiellen Ortsableitungen durch Differenzenquotienten, so dass Sie für die inneren Punkte Folgendes schreiben können:

\[ \frac{\partial \mathbf{y}(t_j)}{\partial t} = A \cdot \mathbf{y}^{j} + \mathbf{b}. \]

Dabei ergeben sich \(A \in \mathbb{R}^{N-1 \times N-1}\) und \(\mathbf{b} \in \mathbb{R}^{N-1}\) aus den verwendeten Differenzenquotienten sowie den Randwerten \(\rho(x_0, t) = \rho_a, \rho(x_N, t) = \rho_b\).
Diskretisieren Sie nun in der Zeit, indem Sie eine Vorschrift

\[ \mathbf{y}^{(j)} = \mathbf{y}^{(j-1)} + \Delta t \phi(\mathbf{y}^{(j)}, \mathbf{y}^{(j-1)}) \]

finden. Je nachdem ob Sie das explizite Euler-Verfahren oder das Crank-Nicolson-Verfahren verwenden, erhalten Sie eine anderen Gestalt für \(\phi\).

Aufgabe 2: Programmierung#

Schreiben Sie ein Matlab-Programm, das die Gleichung (1) für ein beliebiges Zeitinterval \([t_0, t_1]\) und Ortsintervall \([x_0, x_1]\) mit zeitlich konstanten Dirichlet-Randbedingungen \(\rho(x_0, t) = \rho_a, \rho(x_N, t) = \rho_b\) löst. Implementieren Sie sowohl das explizite Euler-Verfahren als auch das Crank-Nicolson-Verfahren.

Visualisieren Sie die Lösung mit Hilfe einer Animation. Unten sehen Sie eine Beispiellösung.

Achtung

Beachten Sie bei der Wahl der Diskretisierung die Courant-Friedrichs-Lewy-Zahl.

Aufgabe 3: CFL Grenzwert#

Prüfen Sie, für welche CFL-Zahl das explizite Euler-Verfahren nicht mehr funktioniert. Stellen Sie durch Ausprobieren auf 2 Nachkommastellen fest, wo der Grenzwert ist. Der Wert liegt vermutlich zwischen 0.1 und 1. Stellen Sie Ihren Code so ein, dass die CFL-Zahl direkt von Ihnen - auf einen klein genugen Wert - festgelegt werden kann.

Aufgabe 4: Zeitabhängige Fließgeschwindigkeit \(c(t)\)#

Erweitern Sie Ihr Programm, so dass die Nutzenden eine zeitabhängige (z.B. pulsierende) Fließgeschwindigkeit \(c(t)\) vorgeben können. Passen Sie gegebenenfalls die Schrittweite an, um die CFL-Zahl einzuhalten.

Ihre Lösungen können beispielsweise für das Parameterset

\(a = 1 \,\frac{\text{m}^2}{\text{s}}\)
\(c_\text{const} = 5 \,\frac{\text{m}}{\text{s}}\)
\(c_\text{dynamic} = (5 + 5\cdot\sin(4\pi \,t/\text{s})) \,\frac{\text{m}}{\text{s}}\)
\(t \in [0, 1 \,\text{s}]\)
\(x \in [0, 10 \,\text{m}]\)
\(dx = 0.05 \,\text{m}\)
\(dt = 1e-4 \,\text{s}\)
\(\rho_a = \rho_b = 0 \,\frac{1}{\text{m}^3}\)
\(\rho(x,0) = \rho_0(x) = 1 \,\frac{1}{\text{m}^3} \,\forall\, x \in [0.2\,\text{m},0.4\,\text{m}]\) so aussehen (nur jeder 50. Zeitschritt wurde ausgegeben):

Abbildung 2: Gegenüberstellung der Lösungen mit explizitem Euler-Verfahren und Crank-Nicolson-Verfahren. Verlauf der Dichte eines diffundierenden Fluids in einem sich bewegenden Fluid. Blau: Konstante Geschwindigkeit. Orange: pulsierende Geschwindigkeit.

Hinweis

Die Parameter sind so gewählt, dass die physikalischen Effekte in der graphischen Ausgabe wahrnehmbar sind. Realistischer wären Parameter wie \(c = 22.88 + 1.58\cdot\sin(2\cdot\pi \,t/\text{s}) \,\frac{\text{cm}}{\text{s}}\) (vgl. [MMDKS17]), \(a\) in der Größenordnung \(10^{-9}\) (vgl. Wikipedia), Strecken in der Größenordnung \(\text{cm}\) und ein Puls von 60-80, statt wie hier 120.

Zusatzaufgabe: Vermeidung numerischer Oszillationen#

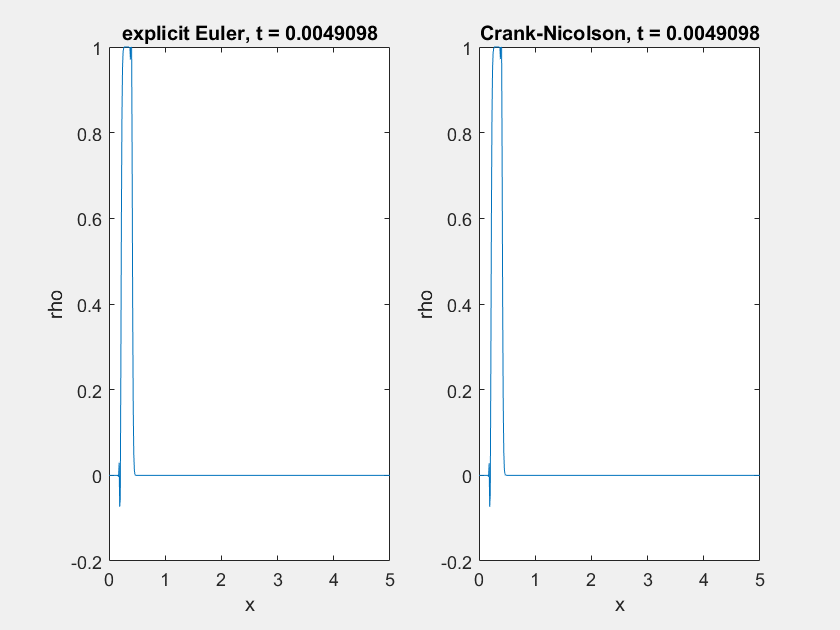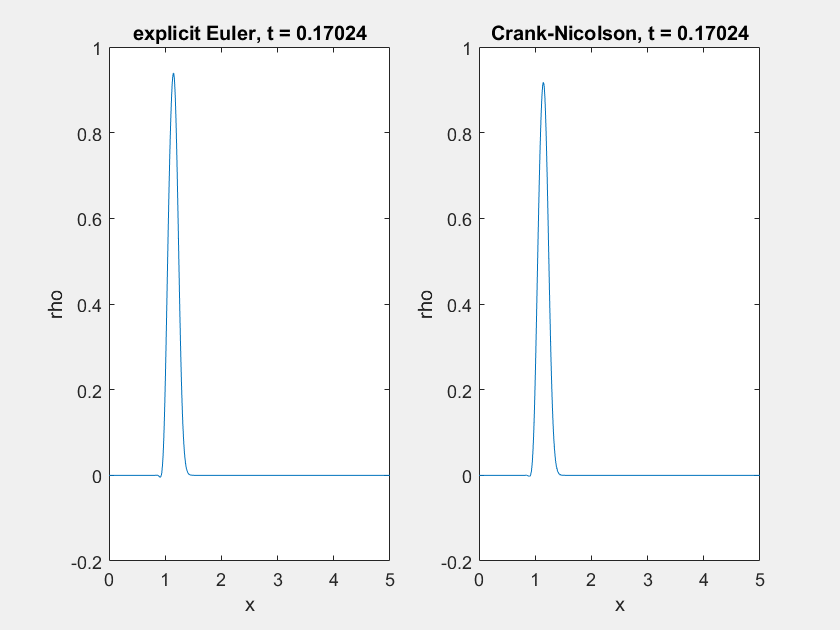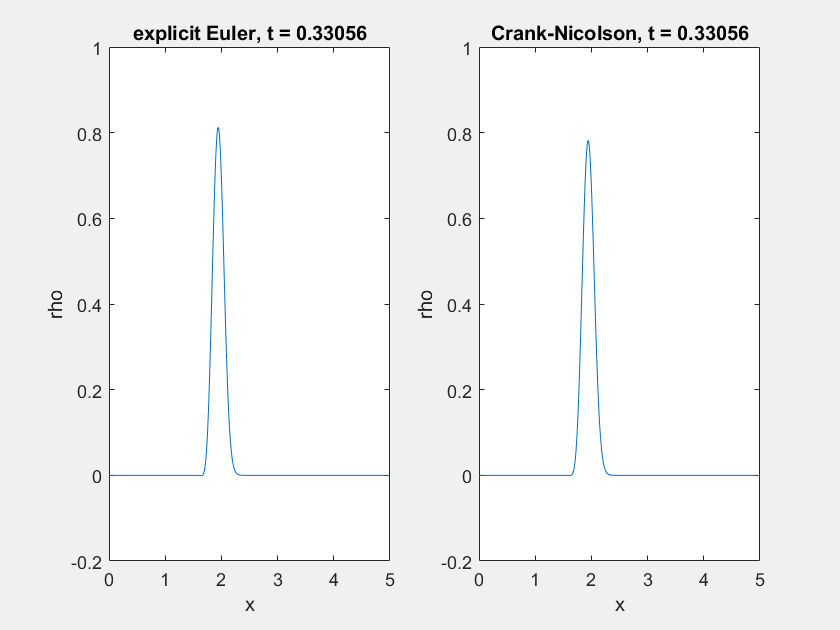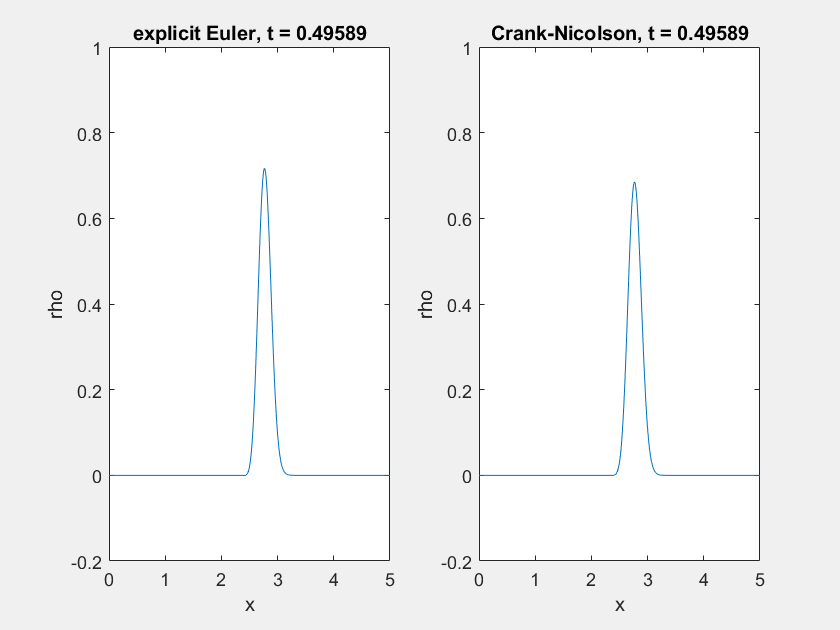
Für \(a \ll 1\) (hier \(a=0.01\)) hängen sich unabhängig von der Lösungsmethode hinter dem “Hauptstrom” Oszillationen an:

Abbildung 3: Gegenüberstellung der Lösungen mit explizitem Euler-Verfahren und Crank-Nicolson-Verfahren mit numerischen Schwingungen. Verlauf der Dichte eines diffundierenden Fluids in einem sich bewegenden Fluid.

Der Ursprung dieser Oszillationen liegt in der Numerik: Die Steilheit der linken Flanke führt dazu, dass die Dichte unter- und später überschätzt wird. Dies lässt sich auch mit einem Differenzenquotienten höherer Ordnung für den Diffusionsanteil nicht lösen. Eine dagegen einfache Abhilfe ist die Verwendung von mehr Ortsschritten (hier \(x_n = 500\) statt \(100\)):

Abbildung 4: Gegenüberstellung der Lösungen mit explizitem Euler-Verfahren und Crank-Nicolson-Verfahren mit weniger numerischen Schwingungen durch feinere Auflösung. Verlauf der Dichte eines diffundierenden Fluids in einem sich bewegenden Fluid.

Hinweis

Weiterführend können Sie sich über ENO (Essentially Non-Oscillatory) Methoden informieren. Diese sind speziell dafür entwickelt, numerische Oszillationen zu vermeiden. Ein Beispiel für eine ENO Methode finden Sie in dem Kapitel Verkehrssimulation mit finiten Volumen.

Literatur#

MMDKS17: Alireza Mohammadkarim, Manijhe Mokhtari-Dizaji, Ali Kazemian, and Hazhir Saberi. Hemodynamic analysis of radiation-induced damage in common carotid arteries by using color doppler ultrasonography. Ultrasonography (Seoul, Korea), 37:, 04 2017. doi:10.14366/usg.17016.