Ctrl+K

9. Differential-Algebraische Gleichungen (1)

9. Differential-Algebraische Gleichungen (1)#

In dieser Übung wird das Rollen einer Kugel auf einer Bahn simuliert. Da die Bewegung der Kugel durch die Bahn eingeschränkt ist, handelt es sich um ein sog. DAE-System (Differential-Algebraic Equation).

Situation#

Eine Kugel rollt eine Bahn hinab. Diese Bahn ist beschrieben durch

\[f(x) = \cos\left(\frac{x}{2}\right)+1\]

Die Kugel kann als DAE-System modelliert und anschließend ihr Rollen auf der Bahn simuliert werden.

1. Kugelbahn#

Stellen Sie für die Bahn der Kugel eine eigene function auf und plotten Sie diese.

% if your Octave kernel does not plot, write `graphics_toolkit("gnuplot")`
%your code here

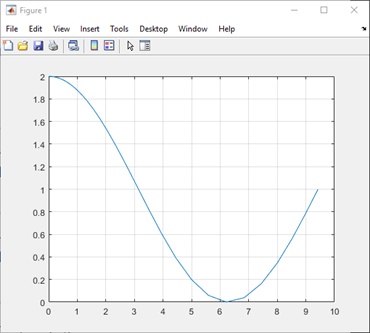
Ihr Ergebnis sollte so aussehen:

sphere rolling curve

2. Modellbildung#

Stellen Sie die Bewegungsgleichungen der Kugel auf. Formulieren Sie dazu die Zwangsbedingung (=Bahn) als Nullstellenproblem.

\[f(x,y)=0\]

Die Bewegungsgleichungen der Kugel ergeben sich aus der Kräftebilanz

\[\begin{split}m \left( \begin{array}{c} \ddot{x}\\ \ddot{y}\\ \end{array} \right) = \vec{F_\text{G}} + \vec{F_\text{R}}\end{split}\]

wobei sich die Zwangskraft \(F_\text{R}\) wie folgt berechnet:

\[\vec{F_\text{R}}=\lambda\cdot\text{grad}(f)\]
\[\begin{split}\text{grad}(f)=\left( \begin{array}{c} \ddot{\frac{\partial f}{\partial{x}}}\\ \ddot{\frac{\partial f}{\partial{y}}}\\ \end{array} \right)\end{split}\]

Nun haben Sie zwei Differentialgleichungen für die \(x\)-\(y\)-Bewegungen. Die Zwangsbedingung \(f(x,y)\) muss nun noch auf Index-1 reduziert werden.

Dazu wird \(f\) zweimal nach der Zeit abgeleitet. Beachten Sie, dass sowohl \(x\) als auch \(y\) zeitabhängige Variablen sind.

Abschließend muss das entstandene System (=3 Gleichungen) auf Ordnung 1 reduziert werden (= 5 Gleichungen), bevor es in Matlab implementiert werden kann. Das zu implementierende System sollte dann folgende Form haben:

\[q_1 = x, q_2 = \dot{x}, q_3 = y, q_4 = \dot{y}, q_5 = \lambda\]

\(\dot{q_1}=q_2\)
\(\dot{q_2}=\dots\)
\(\dot{q_3}=q_3\)
\(\dot{q_4}=\dots\)
\(\dot{q_5}=\frac{d^2}{dt^2}f(x,y)\)

3. Implementierung#

Legen Sie zur Implementierung eine Programmstruktur ähnlich dem Lösen von ODEs an.

function main
    q0 = [0;0.1;2;0;0];
    tspan = [0,15];
    [t,q] = ode15s(@dae,tspan,q0);
end

function dq = dae(t,q)
    % Hier die Systemgleichungen einfügen
end

Zur Lösung benötigt der Solver Kenntnis über die Masse-Matrix des Systems. Diese definiert sich in diesem Fall als Einheitsmatrix, deren letzter Eintrag eine Null ist.

\[\begin{split}M = \begin{pmatrix} 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{pmatrix}\end{split}\]

Definieren Sie daher vor dem Solver-Aufruf die Matrix \(M\) und übergeben Sie diese per folgender Codezeile:

options = odeset('Mass',M);

4. Simulation und Auswertung#

  1. Lassen Sie sich die Simulationsergebnisse als X-Y-Plot ausgeben.

  2. Plotten Sie die vorgegebene Bahnkurve sowie die Ergebnisse der DAE-Berechnung übereinander. Folgt die Kugel auch der Bahn oder gibt es Abweichungen?

  3. Definieren Sie folgende Events:
    Detektion von y == 1, y == 0 und Stopp der Simulation, wenn die Kugel das zweite Mal y == 0 (ca. bei x == 9.4) erreicht.
    Zu welchem Zeitpunkt \(t\) werden diese Werte jeweils erreicht?

% your code here

5. Zusatz: Dämpfung und animierter Plot#

Ergänzen Sie zur Kräftebilanz eine verallgemeinerte Dämpfungskraft \(F_\text{d}=d\cdot\begin{pmatrix}\dot{x}\\\dot{y}\end{pmatrix}\), mit \(d=0.5\), sodass die Kugel nach einer gewissen Zeit zum Stillstand kommt.

Animieren Sie anschließend den Lauf der Kugel, indem Sie mittels for-Schleife die Ergebnisse pro Zeitschritt nacheinander anzeigen lassen.

% if your Octave kernel does not plot, write `graphics_toolkit("gnuplot")`
for i = 1:length(t)
    plot(q(i,1),q(i,3),'x')
    grid on
    axis([0,10,0,2])
    pause(0.05)
    drawnow
end

Lösung#

- Hinweis: Dieses Video ist von YouTube aus eingebunden und nicht Teil des frei lizenzierten Materials! -

Contents