Voraussetzungen
Programmier-Grundlagen
Lerninhalte
schrittweise vertiefte Modellbildung
Nutzung von Unit Tests
Flüssigkeit im Boden#
Erstellen Sie ein Programm, in dem das Versickern einer Flüssigkeit im Boden in 2D modelliert wird. Legen Sie dazu eine Matrix an, die einen Bodenausschnitt mit beliebiger Breite \(w\) und Tiefe \(d\) darstellt. Die Oberfläche des Bodens sei im Bereich \([\frac{w}{4},\frac{3w}{4}]\) mit Flüssigkeit benetzt.
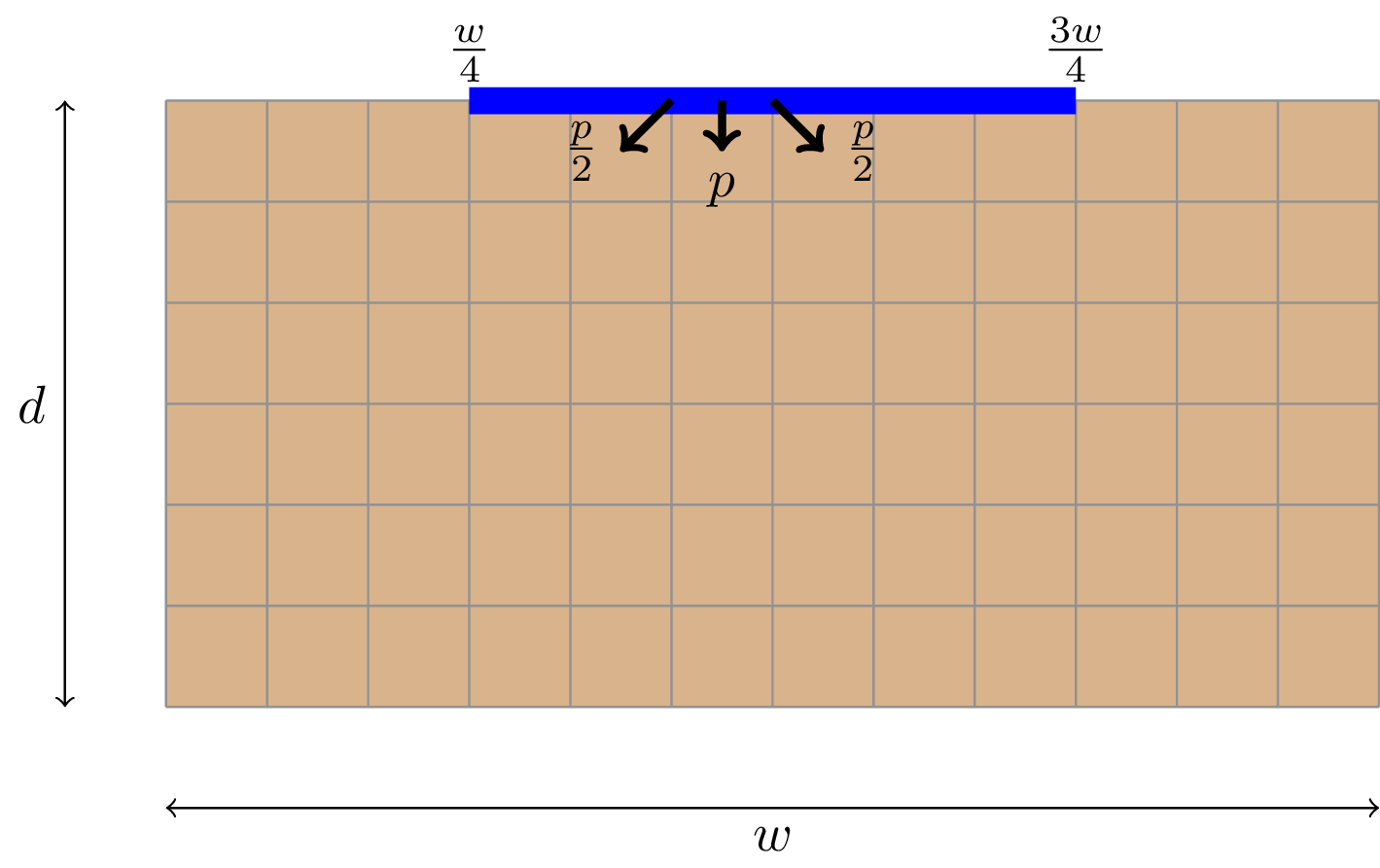
Die Flüssigkeit dringt mit einer Wahrscheinlichkeit \(p\) (Bodenparameter) senkrecht in die nächste Lage des Bodens ein. Zusätzlich kann es passieren, dass die Flüssigkeit in diagonal versetzte Bodenelemente eindringt, jeweils mit der Wahrscheinlichkeit \(\frac{p}{2}\). Als Modellvereinfachung gehen Sie davon aus, dass jede Zelle entweder Flüssigkeit enthält oder nicht, d.h. der Zustand jeder Zelle binär ist.
Aufgabe 1 - Parametrierung des Bodenmodells#
Schreiben Sie eine Matlab-Funktion, die diesen Prozess simuliert:
Anmerkung
Verwenden Sie für jede Funktion ein neues bzw. eigenes .m-file, das nach der Funktion benannt ist. Beispiel: Erstellen Sie für die Funktion ‘groundwater_sim()’ die Datei groundwater_sim.m, die nur diese Funktion enhält. Um die Funktion zu verwenden legen Sie eine neue Datei, zB A1.m, an, die den Funktionsaufruf zu groundwater_sim enthält und führen Sie diese aus.
%%file groundwater_sim.m
function ground = groundwater_sim(depth, width, probability)
% simulate diffusion of groundwater using cellular automata.
%
% The ground is modelled as a rectangular 2D-grid of size
% depth x width.
% Fluid from a cell or the surface propagates to cells below
% according to a certain probability. Initially, the central
% half of the surface is covered by fluid
%
% Inputs:
% - depth: The depth of the regular 2D grid
% - width: The width of the regular 2D grid
% - probability: The seeping probability into lower cells
%
% Outputs:
% - ground: 2D-grid representing the groundwater distribution
% It is a (depth x width) Matrix with values in [0,1]
end
Tipp:
Für die Visualisierung können Sie zum Beispiel die Funktion
spyoderimagescverwenden.Die Ränder der Bodenmatrix sind gesondert zu behandeln.
Wenn Sie möchten, können Sie zur Selbstkontrolle den folgenden Unit Test benutzen, um die Plausibilität der Ergebnisse Ihrer Funktion zu überprüfuen:
moxunit_runtests test_groundwater_sim.m
Den Code hinter test_groundwater_sim.m können Sie hier ausklappen.
Show code cell source
function test_suite=test_groundwater_sim
% initialize unit tets
try
test_functions=localfunctions();
catch
end
initTestSuite;
end
function test_for_logical
% test if result contains only zeros and ones
ground = groundwater_sim(100,100,0.1);
assertElementsAlmostEqual(double(ground), double(logical(ground)));
end
function test_for_correct_size
% test if result contains only zeros and ones
depth = randi(500);
width = randi(500);
ground = groundwater_sim(depth,width,0.1);
assertEqual(size(ground),[depth width]);
end
function test_for_existing_parent
% test if each wetted cell has a origin in the layer above
depth = randi(500);
width = randi(500);
ground = groundwater_sim(depth,width,rand);
for i=2:depth
js = find(ground(i,:));
for j=js
s=max(1,j-1);
e=min(width,j+1);
assert(any(ground(i-1,s:e)));
end
end
end
function test_num_wetted_cells_per_layer_rand
% test if the number of wetted cells in each layer is plausible
ground = groundwater_sim(80,80,rand());
for i=2:80
nwetted_above = sum(ground(i-1,:));
num_puddles = sum(abs(diff(ground(i-1,:))))/2;
nwetted = sum(ground(i,:));
assertTrue(nwetted <= nwetted_above+num_puddles*2);
end
end
function test_num_wetted_cells_per_layer_deterministic
% test if the number of wetted cells in each layer is plausible
% use probability = 2, so that definitely all three cells below a
% wetted cells will be wetted. This makes the simulation
% deterministic;
ground = groundwater_sim(80,80,2);
expected = zeros(80,80);
for i=1:80
first = max([ 1,21-i]);
last = min([80,59+i]);
expected(i,first:last)=1;
end
assertEqual(expected,ground);
end
Parametrieren Sie den Bodenparameter \(p\) so, dass über 1000 Simulationen gemittelt am unteren Ende circa drei Zellen befeuchtet sind. Berechnen Sie dann den Mittelwert und die Standardabweichung. Verwenden Sie hierfür konkret \(d=80\) und \(w=250\). Schreiben Sie dazu ein Matlab-Skript, das die Funktion groundwater_sim verwendet.
Aufgabe 2 - Unregelmäßigkeiten im Boden#
Reale Böden sind in der Regel sehr unregelmäßig strukturiert, sodass Flüssigkeiten an verschiedenen Punkten auch unterschiedlich gut in den Boden eindringen können. Gehen Sie nun davon aus, dass der Boden zu einem Anteil von ratio_absorb aus zufällig verteiltem Material besteht, welches Flüssigkeit absorbieren kann, d.h. die Flüssigkeit am weiteren Versickern im Boden hindert. Modifizieren Sie Ihr Programm aus Aufgabe 1 so, dass diese Unregelmäßigkeit des Bodens zusätzlich berücksichtigt wird.
Geben Sie als zusätzliche Ausgabe die Matrix aus, die das absorbierende Material repräsentiert.
%%file groundwater_sim.m
function [ground, absorb_mat] = groundwater_sim(depth, width, probability, ratio_absorb)
% simulate diffusion of groundwater using cellular automata.
%
% The ground is modelled as a rectangular 2D-grid of size
% depth x width.
% Fluid from a cell or the surface propagates to cells below
% according to a certain probability. Initially, the central
% half of the surface is covered by fluid
%
% Inputs:
% - depth: The depth of the regulear 2D grid
% - width: The width of the regular 2D grid
% - probability: The seeping probability into lower cells
% - ratio_absorb: Ratio of absorbing material in the ground
% values between 0 and 1
%
% Outputs:
% - ground: 2D-grid representing the groundwater distribution
% It is a (depth x width) Matrix with values in {0,1}
% - absorb_mat: 2D-grid representing the absorbing material
% It is a (depth x width) Matrix with values in {0,1}
end
Geben Sie \(p\) aus Aufgabe 1 vor und variieren Sie ratio_absorb ausgehend von 10%. Wie groß muss der Anteil mindestens sein, damit über 1000 Simulationen gemittelt weniger als eine Zelle am unteren Ende des Bodensegments von Flüssigkeit erreicht wird (\(d=80\) und \(w=250\))?
Tipp: Die Matlab-Funktion randperm könnte nützlich sein.
Aufgabe 3 - Einfluss der Tiefe#
In größerer Tiefe ist das Bodenmaterial stärker verdichtet als nahe der Oberfläche. Erweitern Sie Ihr Programm aus Aufgabe 2 so, dass sich die Flüssigkeit bei zunehmender Tiefe schlechter durch den Boden bewegt. Führen Sie einen Parameter depth_influence ein, um die Stärke dieses Effektes zu regulieren. Wichtig: Vergessen Sie nicht in der Dokumentation der Funktion anzugeben, wie dieser Parameter zu verstehen ist und welche Werte erlaubt sind!
Um die Eingabeparameter Ihrer Funktion übersichtlich zu gestalten, sammeln Sie alle Bodenparameter in einem Structure array mit Namen params.
%%file groundwater_sim.m
function [ground, absorb_mat] = groundwater_sim(depth, width, params)
% simulate diffusion of groundwater using cellular automata.
%
% The ground is modelled as a rectangular 2D-grid of size
% depth x width.
% Fluid from a cell or the surface propagates to cells below
% according to a certain probability. Initially, the central
% half of the surface is covered by fluid
%
% Inputs:
% - depth: The depth of the regulear 2D grid
% - width: The width of the regular 2D grid
%
% - params.probability: The seeping probability into
% lower cells
% - params.ratio_absorb: Ratio of absorbing material in
% the ground values between 0 and 1
% - params.depth_influence: influence of the depth on the
% seeping probability (FURTHER EXPLANATION NEEDED!)
%
% Outputs:
% - ground: 2D-grid representing the groundwater distribution
% It is a (depth x width) Matrix with values in {0,1}
% - absorb_mat: 2D-grid representing the absorbing material
% It is a (depth x width) Matrix with values in {0,1}
end
In einem Skript können Sie die Parameter im Structure array speichern und so gesammelt an die Funktion übergeben:
depth = 10;
width = 10;
params.probability = 0.1;
params.ratio_absorb = 0.1;
params.depth_influence = 0.5;
[G, A] = groundwater_sim(depth, width, params);
Aufgabe 4 - Gesteigerter Realismus#
Überlegen Sie sich einen weiteren Einflussparameter mit dem der Prozess des Versickerns realistischer simuliert werden kann und modifizieren Sie Ihr Programm aus Aufgabe 3 entsprechend. In welchen Grenzen kann man diesen Parameter sinnvoll wählen?

